题目内容
 如图所示的三角形数阵叫“莱布尼兹调和三角形”,有
如图所示的三角形数阵叫“莱布尼兹调和三角形”,有| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据已知中“莱布尼兹调和三角形”数阵中所示的规律,我们观察、分析、归纳后,可得每一行的第一数均为行数的倒数,且每一个数等于下一行中“脚踩”的两个数的和,由此分别求出第10行和第11行的第一个数,进而得到第11行第2个数.
解答:解:由“莱布尼兹调和三角形”中数的排列规律,
我们可以推断:
第10行的第一个数为
,
第11行的第一个数为
,
则第11行的第二个数为
-
=
,
故选B
我们可以推断:
第10行的第一个数为
| 1 |
| 10 |
第11行的第一个数为
| 1 |
| 11 |
则第11行的第二个数为
| 1 |
| 10 |
| 1 |
| 11 |
| 1 |
| 110 |
故选B
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
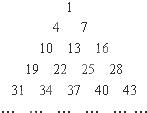 将正整数按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第4个数是( )
将正整数按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第4个数是( )| A、580 | B、577 | C、576 | D、574 |
 如图所示的三角形数阵叫“莱布尼兹调和三角形”,有
如图所示的三角形数阵叫“莱布尼兹调和三角形”,有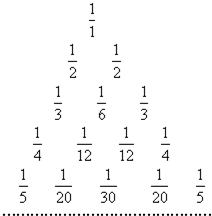 如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第b行有n个数,且第n(n≥2)行两端的数均为
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第b行有n个数,且第n(n≥2)行两端的数均为 已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )
已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( ) 将正整数按一定的规则排成了如图所示的三角形数阵,根据这个排列规则,数阵中第20行从左至右的第5个数是
将正整数按一定的规则排成了如图所示的三角形数阵,根据这个排列规则,数阵中第20行从左至右的第5个数是