题目内容
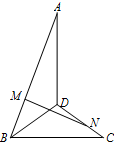 直二面角A-BD-C中,M、N分别是线段AB、CD上的点(不包括端点),且∠ADB=∠DBC=90°,AD=DB=BC=1,AM=DN,AM=x,MN=y.
直二面角A-BD-C中,M、N分别是线段AB、CD上的点(不包括端点),且∠ADB=∠DBC=90°,AD=DB=BC=1,AM=DN,AM=x,MN=y.(1)若MN与平面BCD所成的角为45°,求x的值;
(2)求函数y=f(x)的解析式及定义域、值域.
分析:(1)作ME⊥BD于E,则ME⊥平面BCD,然后根据比例关系可得EN∥BC,然后根据ME=EN建立等式关系,求出x的值即可;
(2)先利用勾股定理求出函数f(x)的解析式,然后根据偶次根式的意义求出定义域,根据二次函数的性质求出函数的值域.
(2)先利用勾股定理求出函数f(x)的解析式,然后根据偶次根式的意义求出定义域,根据二次函数的性质求出函数的值域.
解答: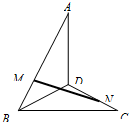 解:(1)作ME⊥BD于E,则ME⊥平面BCD,∴∠MNE=45°,
解:(1)作ME⊥BD于E,则ME⊥平面BCD,∴∠MNE=45°,
=
=
⇒EN∥BC.ME=
(
-x)=1-
x,EN=
x,由ME=EN⇒x=
.
(2)函数解析式y=f(x)=
=
=
,定义域( 0 ,
),值域[
, 1 ).
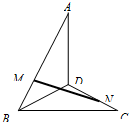 解:(1)作ME⊥BD于E,则ME⊥平面BCD,∴∠MNE=45°,
解:(1)作ME⊥BD于E,则ME⊥平面BCD,∴∠MNE=45°,| DE |
| EB |
| AM |
| MB |
| DN |
| NC |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(2)函数解析式y=f(x)=
| EM2+EN2 |
x2-
|
(x-
|
| 2 |
| ||
| 2 |
点评:本题主要考查了立体几何,解题的关键是将空间问题转化成平面问题,属于中档题.

练习册系列答案
相关题目
将边长为4的正方形ABCD沿对角线BD折成直二面角A-BD-C,若点A、B、C、D都在一个以E为球心的球面上,则球E的体积与面积分别是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示,在平行四边形中,
如图所示,在平行四边形中, 如图,在平行四边形ABCD中,2|AB|2+|BD|2-4=0,∠ABD=90°,沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的表面积是( )
如图,在平行四边形ABCD中,2|AB|2+|BD|2-4=0,∠ABD=90°,沿BD折成直二面角A-BD-C,则三棱锥A-BCD的外接球的表面积是( )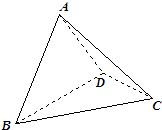 (2007•盐城一模)菱形ABCD中,AB=2,∠BCD=60°,现将其沿对角线BD折成直二面角A-BD-C(如图),则异面直线AB与CD所成角的余弦值为( )
(2007•盐城一模)菱形ABCD中,AB=2,∠BCD=60°,现将其沿对角线BD折成直二面角A-BD-C(如图),则异面直线AB与CD所成角的余弦值为( )