题目内容
已知动点P到点A(-2,0)与点B(2,0)的斜率之积为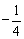 ,点P的轨迹为曲线C。
,点P的轨迹为曲线C。
(Ⅰ)求曲线C的方程;
(Ⅱ)若点Q为曲线C上的一点,直线AQ,BQ与直线x=4分别交于M、N两点,直线BM与椭圆的交点为D。求线段MN长度的最小值。
解:(Ⅰ)设 ,由题意知
,由题意知  ,即
,即
化简得曲线C方程为:
(Ⅱ)思路一
满足题意的直线 的斜率显然存在且不为零,设其方程为
的斜率显然存在且不为零,设其方程为 ,
,

由(Ⅰ)知 ,所以,设直线
,所以,设直线 方程为
方程为
 ,
,
当 时得
时得 点坐标为
点坐标为 ,易求
,易求 点坐标为
点坐标为
所以 =
=
 ,
,
当且仅当 时,线段MN的长度有最小值
时,线段MN的长度有最小值 .
.
思路二:满足题意的直线 的斜率显然存在且不为零,设其方程为
的斜率显然存在且不为零,设其方程为 ,
,
联立方程:
消元得 ,
,
设 ,
, ,
,
由韦达定理得: ,
,
所以 ,代入直线方程得
,代入直线方程得 ,
,
所以 ,又
,又
所以直线BQ的斜率为
以下同思路一
思路三:设 ,则直线AQ方程为
,则直线AQ方程为
直线BQ的方程为
当 ,得
,得 ,即
,即
当 ,得
,得 ,即
,即
则

又
所以
利用导数,或变形为二次函数求其最小值。

练习册系列答案
相关题目
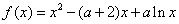 ,其中
,其中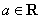 .
.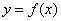 在点
在点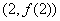 处的切线的斜率为
处的切线的斜率为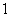 ,求
,求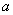 的值;
的值;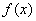 的单调区间.
的单调区间. 关于x的一元二次不等式
关于x的一元二次不等式 的解集中有且仅有3个整数,则所有符合条件的a的值之和是
的解集中有且仅有3个整数,则所有符合条件的a的值之和是 ,则输出
,则输出 的值是
的值是
 是定义在
是定义在 上的单调递增函数,且
上的单调递增函数,且 时,
时, ,若
,若 ,则
,则 ;
;
 中,
中, ,
, ,
, ,那么数列
,那么数列 的前
的前 项和等于
项和等于 (B)
(B) (C)
(C) (D)
(D)
 与圆
与圆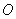 相切于
相切于 ,半径
,半径 ,
, 交
交 于
于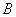 ,若
,若 ,
, ,则
,则 ,
, .
. 
 满足
满足 ,若
,若 的最大值为13,则实数
的最大值为13,则实数 ( )
( )  C.
C.  D. 5
D. 5 中,已知
中,已知 ,则
,则 =
=