题目内容
15．已知$\frac{sinα-2cosα}{cosα+sinα}$=$\frac{1}{4}$，则tanα=3．分析 由条件利用同角三角函数的基本关系，求得要求式子的值．
解答 解：∵$\frac{sinα-2cosα}{cosα+sinα}$=$\frac{tanα-2}{1+tanα}$=$\frac{1}{4}$，
∴tanα=3，
故答案为：3．
点评 本题主要考查同角三角函数的基本关系，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
5．一个算法的程序框图如图所示，该程序输出的结果为$\frac{36}{55}$，则空白处应填入的条件是（ ）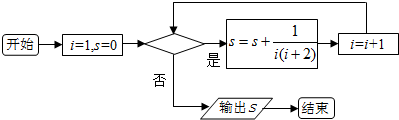
| A． | i≤9 | B． | i≤6 | C． | i≥9 | D． | i≤8 |
6．已知iz=2+i，则z的共轭复数在复平面内对应点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
3．已知实数x，y满足不等式组$\left\{\begin{array}{l}{x+2y-2≥0}\\{x-2y+2≥0}\\{x≤2}\end{array}\right.$，则目标函数z=2x+y的最大值为（ ）
| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
20．执行如图所示的程序框图，则输出的结果s是（ ）
| A． | 15 | B． | 105 | C． | 126 | D． | 945 |