题目内容
已知函数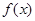 满足对任意的
满足对任意的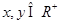 恒有
恒有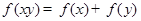 ,且当
,且当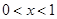 时,
时,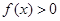 .
.
(1)求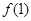 的值;
的值;
(2)判断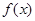 的单调性
的单调性
(3)若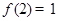 ,解不等式
,解不等式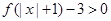 .
.
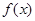 满足对任意的
满足对任意的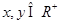 恒有
恒有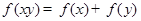 ,且当
,且当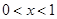 时,
时,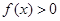 .
.(1)求
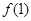 的值;
的值;(2)判断
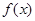 的单调性
的单调性(3)若
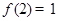 ,解不等式
,解不等式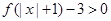 .
.(1) ;(2)
;(2) 在
在 单调递减;(3)
单调递减;(3) .
.
 ;(2)
;(2) 在
在 单调递减;(3)
单调递减;(3) .
.试题分析:(1)采用附值:将
 代入
代入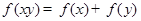 即可出
即可出 ;(2)由题中条件
;(2)由题中条件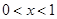 时,
时,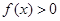 ,先设
,先设 ,进而得到
,进而得到 ,由函数单调性的定义,转为判断
,由函数单调性的定义,转为判断 的符号即可,而
的符号即可,而 ,进而可得
,进而可得 ,这样即可得到
,这样即可得到 在
在 的单调性;(3)先由
的单调性;(3)先由 推出
推出 ,进而结合(2)中函数
,进而结合(2)中函数 的单调性,可将不等式
的单调性,可将不等式 ,进而求解不等式即可.
,进而求解不等式即可.(1)令
 ,可得
,可得 ,即
,即
故
 3分
3分(2)任取
 ,且
,且 ,则
,则
由于当
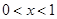 时,
时,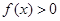 ,∴
,∴ 5分
5分
∴


∴函数
 在
在 上是单调递减函数 8分
上是单调递减函数 8分(3)由
 得
得
∴
 10分
10分 函数
函数 在区间
在区间 上是单调递减函数
上是单调递减函数∴不等式






∴不等式的解集为
 14分.
14分.
练习册系列答案
相关题目
 若对于任一实数
若对于任一实数 ,
, 与
与 至少有一个为负数,则实数
至少有一个为负数,则实数 的取值范围是
的取值范围是  在
在 上单调递增,则实数
上单调递增,则实数 的取值范围为( )
的取值范围为( )



 )=
)= ,则f(x)的值域为( )
,则f(x)的值域为( ) ,+∞)
,+∞) ,且
,且 ,则
,则 等于_____________.
等于_____________. ( )
( )