题目内容
8.不等式x2-3x+1≤0的解集是( )| A. | {x|x≥$\frac{3-\sqrt{5}}{2}$} | B. | {x|x≤$\frac{3+\sqrt{5}}{2}$} | C. | {x|$\frac{3-\sqrt{5}}{2}$≤x≤$\frac{3+\sqrt{5}}{2}$} | D. | ∅ |
分析 根据一元二次不等式的解法步骤,计算△求出对应方程的实数根,写出不等式的解集.
解答 解:不等式x2-3x+1≤0,
△=(-3)2-4×1×1=5,
∴该不等式对应方程的两个实数解为$\frac{3-\sqrt{5}}{2}$和$\frac{3+\sqrt{5}}{2}$,
∴该不等式的解集为{x|$\frac{3-\sqrt{5}}{2}$≤x≤$\frac{3+\sqrt{5}}{2}$}.
故选:C.
点评 本题考查了一元二次不等式的解法与应用问题,是基础题目.

练习册系列答案
相关题目
16.已知k∈Z,角的终边只落在y轴正半轴上的角是( )
| A. | $\frac{kπ}{2}$ | B. | kπ+$\frac{π}{2}$ | C. | 2kπ+$\frac{π}{2}$ | D. | 2kπ-$\frac{π}{2}$ |
3.定义域为R的函数f(x)满足以下条件:
(1)对于任意x∈R,f(x)+f(-x)=0;
(2)对于任意x1、x2∈[1,3],当x2>x1时,有f(x2)>f(x1)>0;
则以下不等式不一定成立的是( )
(1)对于任意x∈R,f(x)+f(-x)=0;
(2)对于任意x1、x2∈[1,3],当x2>x1时,有f(x2)>f(x1)>0;
则以下不等式不一定成立的是( )
| A. | f(2)>f(0) | B. | f(2)>f(1) | C. | f(-3)<f(-1) | D. | f(4)>f(2) |
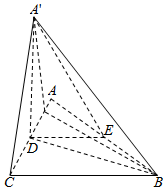 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到四棱锥A′-BCDE,已知A′H⊥CD,垂足为H.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到四棱锥A′-BCDE,已知A′H⊥CD,垂足为H.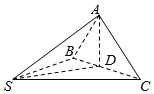 如图所示,在四面体S-ABC中,SA=SB=SC=1,∠ASB=∠ASC=60°,∠BSC=90°,D是BC的中点.求证:
如图所示,在四面体S-ABC中,SA=SB=SC=1,∠ASB=∠ASC=60°,∠BSC=90°,D是BC的中点.求证: