Question

设函数f（x）=log₂[x²-2（a-1）x+b²]的定义域为D．
（1）若a是从1，2，3，4四个数中任取的一个数，b是从1，2，3三个数中任取一个数，求使D=R得概率
（2）若a是从区间[0，4]任取的一个数，b是从区间[0，3]任取的一个数，求使D=R的概率．

Answer 1

分析：（1）由题意可得，D=R 即△=[-2（a-1）]²-4b²＜0，即a-1＜b，由此求得满足此条件的（a，b）共有6个．而所有的（a，b）共有4×3个，由此求得D=R的概率．
（2）由题意可得，△=[-2（a-1）]²-4b²＜0，根据a、b的范围，只要a-1＜b就可以了．所有的（a，b）构成矩形区域OABC，再画出b＞a-1的区域，它们相交的部分（即图中阴影部分），再用阴影部分的面积除以矩形OABC的面积，即得所求．

解答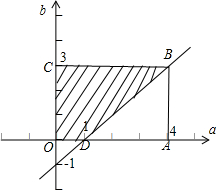：解：（1）由函数f（x）=log₂[x²-2（a-1）x+b²]，
D=R，可得 x²-2（a-1）x+b²]＞0恒成立，
故有△=[-2（a-1）]²-4b²＜0．
再由a、b为正整数，故只要a-1＜b就可以了．
所有的（a，b）共有4×3=12种，
∴

a=1 b=1

、或

a=1 b=2

、或

a=2 b=2

、或

a=1 b=3

、或 

a=2 b=3

、或

a=3 b=3

，共计6种情况．
故D=R的概率为

6

12

=

1

2

．
（2）由题意可得，△=[-2（a-1）]²-4b²＜0．
再由a是从区间[0，4]任取的一个数，b是从区间[0，3]任取的一个数，
故只要a-1＜b就可以了．
以a为横坐标，b为纵坐标画图，画出a属于[0，4]，b属于[0，3]的矩形区域OABC，
画出b＞a-1的区域，它们相交的部分（即图中阴影部分）的面积是4×3-

1

2

×3×3=

15

2

，
而矩形的面积是12，所以D=R的概率是

15 2

12

=

5

8

．

点评：本题主要考查几何概型，体现了转化的数学思想，属于基础题．