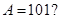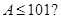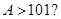题目内容
已知函数f(x)=x2-(1+2a)x+aln x(a为常数).
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.
(1)y=2x.
(2)函数f(x)的单调增区间是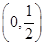 ,单调减区间是
,单调减区间是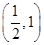 .
.
(2)函数f(x)的单调增区间是
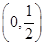 ,单调减区间是
,单调减区间是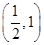 .
.解:(1)当a=-1时,f(x)=x2+x-ln x,
则f′(x)=2x+1-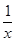 ,
,
所以f(1)=2,且f′(1)=2.
所以曲线y=f(x)在x=1处的切线的方程为
y-2=2(x-1),即y=2x.
(2)由题意得f′(x)=2x-(1+2a)+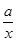
=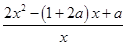
= (x>0).
(x>0).
由f′(x)=0,得x1= ,x2=a.
,x2=a.
①当0<a< 时,由f′(x)>0且x>0,
时,由f′(x)>0且x>0,
得0<x<a或 <x<1;
<x<1;
由f′(x)<0且x>0,得a<x< .
.
所以函数f(x)的单调递增区间是(0,a)和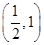 ,单调递减区间是
,单调递减区间是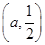 ;
;
②当a= 时,f′(x)=
时,f′(x)=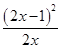 ≥0,当且仅当x=
≥0,当且仅当x= 时,
时,
f′(x)=0.
所以函数f(x)在区间(0,1)上是单调递增函数;
③当 <a<1时,由f′(x)>0且x>0,
<a<1时,由f′(x)>0且x>0,
得0<x< 或a<x<1;
或a<x<1;
由f′(x)<0且x>0,得 <x<a.
<x<a.
所以函数f(x)的单调递增区间是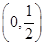 和(a,1),单调递减区间是
和(a,1),单调递减区间是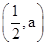 ;
;
④当a≥1时,由f′(x)>0且x>0,
得0<x< ;
;
由f′(x)<0且x>0,得 <x<1.
<x<1.
所以函数f(x)的单调增区间是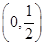 ,单调减区间是
,单调减区间是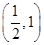 .
.
则f′(x)=2x+1-
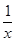 ,
,所以f(1)=2,且f′(1)=2.
所以曲线y=f(x)在x=1处的切线的方程为
y-2=2(x-1),即y=2x.
(2)由题意得f′(x)=2x-(1+2a)+
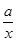
=
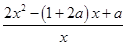
=
 (x>0).
(x>0).由f′(x)=0,得x1=
 ,x2=a.
,x2=a. ①当0<a<
 时,由f′(x)>0且x>0,
时,由f′(x)>0且x>0,得0<x<a或
 <x<1;
<x<1;由f′(x)<0且x>0,得a<x<
 .
.所以函数f(x)的单调递增区间是(0,a)和
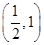 ,单调递减区间是
,单调递减区间是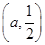 ;
;②当a=
 时,f′(x)=
时,f′(x)=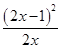 ≥0,当且仅当x=
≥0,当且仅当x= 时,
时,f′(x)=0.
所以函数f(x)在区间(0,1)上是单调递增函数;
③当
 <a<1时,由f′(x)>0且x>0,
<a<1时,由f′(x)>0且x>0,得0<x<
 或a<x<1;
或a<x<1;由f′(x)<0且x>0,得
 <x<a.
<x<a.所以函数f(x)的单调递增区间是
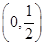 和(a,1),单调递减区间是
和(a,1),单调递减区间是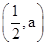 ;
;④当a≥1时,由f′(x)>0且x>0,
得0<x<
 ;
;由f′(x)<0且x>0,得
 <x<1.
<x<1.所以函数f(x)的单调增区间是
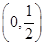 ,单调减区间是
,单调减区间是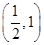 .
.
练习册系列答案
相关题目
 .
.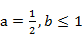 时,
时,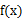 与
与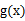 )在定义域上单调性相反,求的
)在定义域上单调性相反,求的 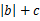 的最小值。
的最小值。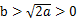 时,求证:存在
时,求证:存在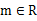 ,使
,使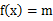 的三个不同的实数解
的三个不同的实数解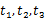 ,且对任意
,且对任意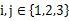 且
且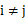 都有
都有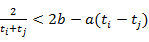 .
.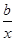 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0. 满足:
满足: 记y=f(x).
记y=f(x). 不等式
不等式 恒成立,求实数a的取值范围:
恒成立,求实数a的取值范围: 上的连续函数
上的连续函数 的导函数为
的导函数为 ,如果
,如果 使得
使得 ,则称
,则称 为区间
为区间 ;②
;② ;③
;③ ;④
;④ 在区间
在区间 上“中值点”多于一个的函数序号为 .
上“中值点”多于一个的函数序号为 .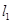 平行直线
平行直线 , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程. 在
在 及
及 处取得极值.
处取得极值. 、
、 的值;(2)求
的值;(2)求 的单调区间.
的单调区间.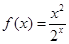 在区间
在区间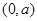 内单调,则
内单调,则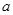 的最大值为__________.
的最大值为__________.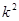 ,若
,若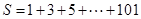 ( )
( )