题目内容
设向量
=（cosθ，sinθ），其中0≤θ≤
，
=（
，1）
（1）若|
|=
，求tanθ的值；
（2）求△POQ面积的最大值．
| OP |
| π |
| 2 |
| OQ |
| 3 |
（1）若|
| PQ |
| 5 |
（2）求△POQ面积的最大值．
考点：平面向量数量积的运算,正弦定理
专题：平面向量及应用
分析：（1）求出
以及模用θ的三角函数表示，然后展开变形求tanθ；
（2）利用三角形的面积公式得到共有θ的正弦解析式，求最大值．
| PQ |
（2）利用三角形的面积公式得到共有θ的正弦解析式，求最大值．
解答：
解：（1）由题意，得
=
-
=（
-cosθ，-1-sinθ），
|
|2═（
-cosθ）2+（-1-sinθ）2=5-2
cosθ+2sinθ=5，
所以tanθ=
…（6分）
（2）因为0≤θ≤
，S△POQ=
×2×1×sin（θ+
）=sin（θ+
），
所以当θ=
时，S△POQ最大值是1，…（12分）
| PQ |
| OQ |
| OP |
| 3 |
|
| PQ |
| 3 |
| 3 |
所以tanθ=
| 3 |
（2）因为0≤θ≤
| π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
所以当θ=
| π |
| 3 |
点评：本题考查了向量的加减法的左边运算以及三角形面积公式、正弦函数性质的运用．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
若函数f（x）=（1+cosx）10+（1-cosx）10，x∈[0，π]，则其最大值等于（ ）
| A、2048 | B、512 |
| C、2 | D、1024 |
设△ABC的三个内角A，B，C所对的边分别为a，b，c，若△ABC的面积S=c2-（a-b）2，则sinC的值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图是函数f（x）=Asin（ωx+φ）（A＞0，0＜ω＜3，0＜φ＜π）的图象的一部分，则ωφ=（ ）
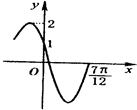
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）=sin（2x+φ），其中φ为实数，若f（x）≤f（
），对x∈R恒成立，且f（
）＜f（π），则f（x）的单调递增区间是（ ）
| π |
| 6 |
| π |
| 2 |
A、[kπ-
| ||||
B、[kπ，kπ+
| ||||
C、[kπ+
| ||||
D、[kπ-
|