题目内容
.已知函数f(x)=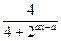 在[0,1]上的最小值为
在[0,1]上的最小值为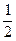 ,
,
(1)求f(x)的解析式; (2)证明:f(1)+f(2)+…+f(n)>n-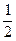 +
+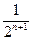 (n∈N
(n∈N )
)
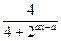 在[0,1]上的最小值为
在[0,1]上的最小值为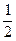 ,
,(1)求f(x)的解析式; (2)证明:f(1)+f(2)+…+f(n)>n-
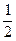 +
+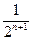 (n∈N
(n∈N )
) (1)f(x)=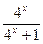 (2)同解析
(2)同解析
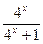 (2)同解析
(2)同解析1)∵a=0时f(x)=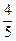 不合题意 ∴a≠0
不合题意 ∴a≠0
此时f(x)在[0,1]上是单调函数
又f(1)=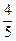 >
>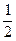 ∴f(x)为单调递增函数 ∴a<0
∴f(x)为单调递增函数 ∴a<0
由f(x)=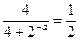 即f(x)=
即f(x)=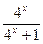
(2)∵f(n)=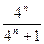 =1-
=1-
>1-
∴f(1)+f(2)+…+f(n) >1-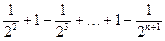
=n-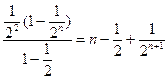
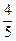 不合题意 ∴a≠0
不合题意 ∴a≠0此时f(x)在[0,1]上是单调函数
又f(1)=
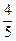 >
>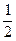 ∴f(x)为单调递增函数 ∴a<0
∴f(x)为单调递增函数 ∴a<0由f(x)=
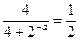 即f(x)=
即f(x)=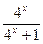
(2)∵f(n)=
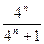 =1-
=1-
>1-

∴f(1)+f(2)+…+f(n) >1-
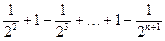
=n-
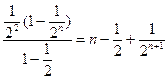

练习册系列答案
相关题目
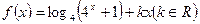 是偶函数.
是偶函数.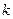 的值;
的值;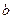 ,函数
,函数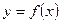 的图象与直线
的图象与直线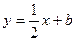 最多只有一个交点.
最多只有一个交点.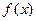 是定义在
是定义在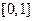 上的函数,若存在
上的函数,若存在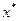
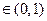 ,使得
,使得 上单调递增,在
上单调递增,在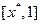 上单调递减,则称
上单调递减,则称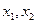
 ,若
,若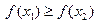 ,则
,则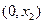 为含峰区间;若
为含峰区间;若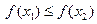 ,则
,则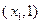 为含峰区间;
为含峰区间; ,证明:存在
,证明:存在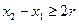 ,使得由(1)所确定的含峰区间的长度不大于
,使得由(1)所确定的含峰区间的长度不大于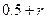 ;
; 上规划出一块长方形地面建造公园,公园一边落在CD上,但不得越过文物保护区
上规划出一块长方形地面建造公园,公园一边落在CD上,但不得越过文物保护区 的EF.问如何设计才能使公园占地面积最大,并求这最大面积.( 其中AB=200m,BC=160m,AE=60m,AF=40m.)
的EF.问如何设计才能使公园占地面积最大,并求这最大面积.( 其中AB=200m,BC=160m,AE=60m,AF=40m.)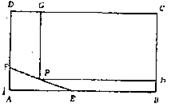
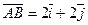 (
(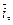
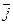 分别是与x轴和y轴正半轴同方向的单位向量),函数g(x)=
分别是与x轴和y轴正半轴同方向的单位向量),函数g(x)=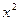 ―x―6,
―x―6,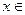 M时,求函数
M时,求函数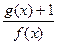 的最小值
的最小值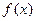 的定义域为R,对任意的
的定义域为R,对任意的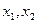 都满足
都满足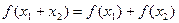 ,当
,当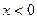 时,
时,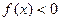 .
.
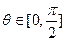 时,使不等式
时,使不等式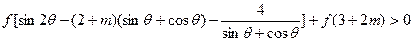
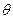 恒成立,如存在,求出m的取值范围;若不存在,说明理由.
恒成立,如存在,求出m的取值范围;若不存在,说明理由.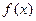
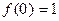
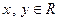
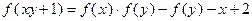 .
.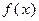 的解析式;
的解析式;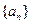 满足:
满足: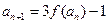 (
(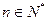 ),且
),且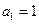 , 求数列
, 求数列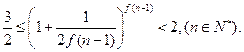
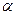 ,
,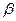 分别是关于
分别是关于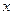 的方程
的方程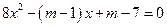 的两个根,且
的两个根,且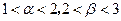 ,求实数
,求实数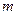 的取值范围.
的取值范围.