题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x},x>0}\\{{x}^{2}-4x,x≤0}\end{array}\right.$,若f(x)≥ax-1恒成立,则实数的取值范围是-2≤a≤0.分析 绘出函数图象,利用数形结合的思想判断a的范围,找出临界点即相切时a的取值,进而得出a的范围.
解答 解:绘制函数图象如图:
由图象可知:
要使f(x)≥ax-1恒成立,
只需函数g(x)=ax-1的图象恒在图象f(x)的下方,
∴a≤0,
设g(x)=ax-1与函数f(x)=x2-4x相切与点P(m,n),
∴m2-4m=(2m-4)m-1,
∴m=1,a=-2,
∴-2≤a≤0.
故答案为:-2≤a≤0.
点评 考查了分段函数和利用导数的定义求切线的斜率.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
15.某几何体的三视图如图所示,且该几何体的体积是$\frac{3}{2}$,则正视图中的x的值是( )
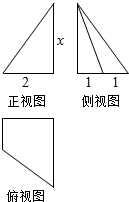

| A. | 2 | B. | $\frac{9}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
16.定义在R上的函数f(x)满足f(x+1)=2f(x),且当0≤x≤1时,f(x)=x2-x,则$f({-\frac{3}{2}})$=( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{1}{4}$ | C. | $-\frac{1}{8}$ | D. | $-\frac{1}{16}$ |
17.已知集合A={x|-3<x<2},B={x|3x>1},则A∩(∁RB)=( )
| A. | (-3,1] | B. | (1,2) | C. | (-3,0] | D. | [1,2) |
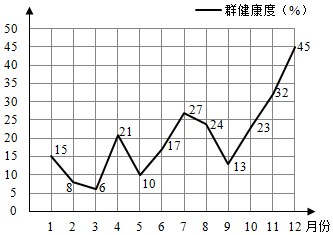 目前很多朋友都加入了微信群,大多数群成员认为有思想的群不仅仅是群里的人转发与主题有关的网页文章,而且群成员之间还有文字或语音的交流,因此规定$\frac{网页类型分享}{文字语音聊天}$为“群健康度”,为此群主统计了一年的群里聊天记录(假定该群进群由群主同意邀请,且无插入广告),并将聊天记录中的网页类型分享和文字语音聊天内容进行了分类统计,并按照“群健康度”制作了分析趋势图,假定“群健康度”小于20%为群氛围优良,“群健康度”大于30%为群氛围不合理.
目前很多朋友都加入了微信群,大多数群成员认为有思想的群不仅仅是群里的人转发与主题有关的网页文章,而且群成员之间还有文字或语音的交流,因此规定$\frac{网页类型分享}{文字语音聊天}$为“群健康度”,为此群主统计了一年的群里聊天记录(假定该群进群由群主同意邀请,且无插入广告),并将聊天记录中的网页类型分享和文字语音聊天内容进行了分类统计,并按照“群健康度”制作了分析趋势图,假定“群健康度”小于20%为群氛围优良,“群健康度”大于30%为群氛围不合理.