题目内容
20．已知f（x）是定义在R上的偶函数．当x≥0时，f（x）=$\frac{2x-3}{x+1}$，则不等式f（lnx）＜l的解集为（$\frac{1}{{e}^{4}}$，e4）．分析 根据函数奇偶性和单调性的关系，将不等式进行转化进行求解即可．
解答 解：∵f（x）是定义在R上的偶函数，
∴不等式f（lnx）＜l等价为f（|lnx|）＜l，
当x≥0时，f（x）=$\frac{2x-3}{x+1}$=$\frac{2（x+1）-5}{x+1}$=2-$\frac{5}{x+1}$，则函数f（x）为增函数，
由f（x）=$\frac{2x-3}{x+1}$=1，得x=4，即f（4）=1，
则不等式f（|lnx|）＜l等价为f（|lnx|）＜f（4），
则|lnx|＜4，
即-4＜lnx＜4，
即$\frac{1}{{e}^{4}}$＜x＜e4，
即不等式的解集为（$\frac{1}{{e}^{4}}$，e4），
故答案为：（$\frac{1}{{e}^{4}}$，e4）
点评 本题主要考查不等式的求解，根据条件判断函数的单调性，利用函数单调性和奇偶性的关系将不等式进行转化是解决本题的关键．
练习册系列答案
相关题目
10．已知f（x）对任意x∈[0，+∞）都有f（x+1）=-f（x），且当x∈[0，1）时，f（x）=x，若函数g（x）=f（x）-loga（x+1）（0＜a＜1）在区间[0，4]上有两个零点，则实数a的取值范围是（ ）
| A． | [$\frac{1}{4}$，$\frac{1}{3}$] | B． | [$\frac{1}{4}$，$\frac{1}{3}$） | C． | [$\frac{1}{5}$，$\frac{1}{3}$） | D． | [$\frac{1}{5}$，$\frac{1}{3}$] |
11．
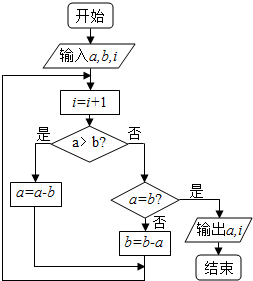如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b，i的值分别为6，8，0，则输出a和i的值分别为（ ）
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b，i的值分别为6，8，0，则输出a和i的值分别为（ ）| A． | 0，3 | B． | 0，4 | C． | 2，3 | D． | 2，4 |
9．已知函数f（x）=Asin（ωx+φ）的图象如图所示，则该函数的解析式可能是（ ）
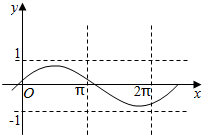
| A． | f（x）=$\frac{3}{4}$sin（$\frac{3}{2}$x+$\frac{π}{6}$） | B． | f（x）=$\frac{4}{5}$sin（$\frac{4}{5}$x+$\frac{1}{5}$） | C． | f（x）=$\frac{4}{5}$sin（$\frac{5}{6}$x+$\frac{π}{6}$） | D． | f（x）=$\frac{4}{5}$sin（$\frac{2}{3}$x-$\frac{1}{5}$） |
10．为了判定两个分类变量X和Y是否有关系，应用K2独立性检验法算得K2的观测值为5，又已知P（K2≥3.841）=0.05，P（K2≥6.635）=0.01，则下列说法正确的是（ ）
| A． | 有95%的把握认为“X和Y有关系” | B． | 有95%的把握认为“X和Y没有关系” | ||
| C． | 有99%的把握认为“X和Y有关系” | D． | 有99%的把握认为“X和Y没有关系” |