题目内容
设a3+b3=2,求证a+b≤2.
思路分析:待证不等式中有小于等于号,不妨试用反证法,在假设a>2-b的情况下,结合a3+b3=2,构造完全平方式,出现矛盾不等式,问题得证.
证明:假设a+b>2,则有a>2-b,从而a3>8-12b+6b2-b3,
a3+b3>6b2-12b+8=6(b-1)2+2.
因为6(b-1)2+2≥2,所以a3+b3>2,这与题设条件a3+b3=2矛盾,所以,原不等式a+b≤2成立.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
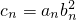 ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn; ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn;