题目内容
13．设x1、x2是方程x2+3$\sqrt{3}$x+4=0的两根，求arctanx1+arctanx2的值．分析 由条件利用韦达定理求得x1+x2 =-3$\sqrt{3}$，x1•x2=4，再利用两角和的正切公式求得tan（arctanx1+arctanx2）的值，可得arctanx1+arctanx2 的值．
解答 解：由x1、x2是方程x2+3$\sqrt{3}$x+4=0的两根，可得x1+x2 =-3$\sqrt{3}$，x1•x2=4，
故x1、x2均小于零，故arctanx1+arctanx2∈（-π，0），
且tan（arctanx1+arctanx2）=$\frac{{tan（arctanx}_{1}{）+tan（arctanx}_{2}）}{1-tan（arcta{nx}_{1}）•tan（arcta{nx}_{2}）}$=$\frac{{x}_{1}{+x}_{2}}{1{-x}_{1}{•x}_{2}}$=$\sqrt{3}$，
∴arctanx1+arctanx2=-$\frac{2π}{3}$．
点评 本题主要考查韦达定理，两角和的正切公式，属于中档题．
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
8．
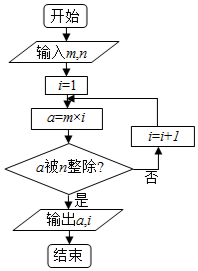当m=4，n=3时，运行如图所示的程序框图，将输出的a、i代入二项式（x2-$\frac{i}{x}$）a中，则此二项式的展开式中含x3项的系数为（ ）
当m=4，n=3时，运行如图所示的程序框图，将输出的a、i代入二项式（x2-$\frac{i}{x}$）a中，则此二项式的展开式中含x3项的系数为（ ）| A． | 37${C}_{12}^{7}$ | B． | 38${C}_{12}^{8}$ | C． | -33${C}_{12}^{3}$ | D． | -37${C}_{12}^{5}$ |
18．过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a，b＞0）$的右焦点F作渐近线的垂线，垂足为P，过P作y轴的垂线交另一渐近线为Q，若△OFP的面积是△OPQ的面积的4倍，则双曲线的离心率为（ ）
| A． | $\frac{\sqrt{5}}{2}$ | B． | $\sqrt{2}$ | C． | 2$\sqrt{2}$ | D． | $\sqrt{5}$ |