题目内容
将一根长为3m的木棒随机折成三段，折成的这三段木棒能够围成三角形的概率是（ ）
A． | B． | C． | D． |
C
解析试题分析：设这三段分别为，
，则
.若能构成三角形，则还应满足：
即
.作出以上不等式组表示的区域，由几何概型的概率公式得
.选C.
考点：1、几何概型；2、不等式组表示的区域.
练习册系列答案
相关题目
已知点
满足条件
，则
的最小值为（ ）
A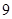． | B． | C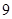．- | D． |
已知实数x，y满足
，则r的最小值为（ ）
| A．1 | B． | C． | D． |
定义
设实数
满足约束条件
则
的取值范围是（ ）
A． | B． | C． | D． |
若变量x,y满足约束条件
则
的最大值为
| A．4 | B．3 | C．2 | D．1 |
已知x,y满足约束条件
,则
的最小值为( )
A． ; | B． ; | C．1 ; | D．3 ; |
已知约束条件
，若目标函数
恰好在点
处取得最大值，则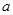
的取值范围为 （ ）
A． | B． | C． | D． |
已知a＞0，x，y满足约束条件
若z＝2x＋y的最小值为1，则a＝（ ）
A． | B． | C．1 | D．2 |
＝α·
＋β·
，则α＋β的最大值是( )
