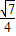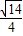题目内容
设点P是椭圆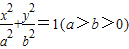 与圆x2+y2=3b2的一个交点,F1,F2分别是椭圆的左、右焦点,且|PF1|=3|PF2|,则椭圆的离心率为( )
与圆x2+y2=3b2的一个交点,F1,F2分别是椭圆的左、右焦点,且|PF1|=3|PF2|,则椭圆的离心率为( )A.
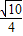
B.

C.
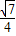
D.
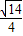
【答案】分析:先由椭圆的定义和已知求出两个焦半径的长,利用余弦定理得关于a、c的等式,然后求得离心率.
解答:解:依据椭圆的定义:|PF1|+|PF2|=2a,又∵|PF1|=3|PF2|,
∴|PF1|= a,|PF2|=
a,|PF2|= a,
a,
∵圆x2+y2=3b2的半径r= b,
b,
∴三角形F1PF2中有余弦定理可得: ,
,
 ,
,
可得7a2=8c2,得e= .
.
故选 D.
点评:本题考查了椭圆的定义,椭圆的几何性质,余弦定理的应用,离心率的求法,考查计算能力.
解答:解:依据椭圆的定义:|PF1|+|PF2|=2a,又∵|PF1|=3|PF2|,
∴|PF1|=
 a,|PF2|=
a,|PF2|= a,
a,∵圆x2+y2=3b2的半径r=
 b,
b,∴三角形F1PF2中有余弦定理可得:
 ,
, ,
,可得7a2=8c2,得e=
 .
.故选 D.
点评:本题考查了椭圆的定义,椭圆的几何性质,余弦定理的应用,离心率的求法,考查计算能力.

练习册系列答案
相关题目
 与圆x2+y2=3b2的一个交点,F1,F2分别是椭圆的左、右焦点,且|PF1|=3|PF2|,则椭圆的离心率为
与圆x2+y2=3b2的一个交点,F1,F2分别是椭圆的左、右焦点,且|PF1|=3|PF2|,则椭圆的离心率为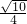


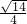
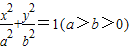 与圆x2+y2=3b2的一个交点,F1,F2分别是椭圆的左、右焦点,且|PF1|=3|PF2|,则椭圆的离心率为( )
与圆x2+y2=3b2的一个交点,F1,F2分别是椭圆的左、右焦点,且|PF1|=3|PF2|,则椭圆的离心率为( )