题目内容
已知定义在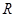 的函数
的函数
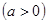 在区间
在区间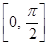 上的值域为
上的值域为 ,
,
(Ⅰ)求 、
、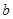 的值;
的值;
(Ⅱ)求函数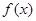 的最小正周期;
的最小正周期;
(Ⅲ)求函数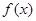 的单调减区间.
的单调减区间.
(Ⅰ) 、
、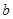 的值分别为3,
的值分别为3,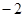 (Ⅱ)
(Ⅱ) (Ⅲ)
(Ⅲ)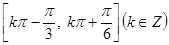
解析试题分析:(Ⅰ)
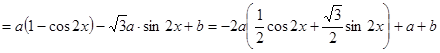
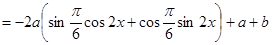
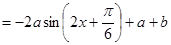
∵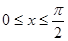 ,∴
,∴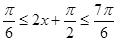 ,∴
,∴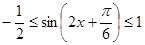 ,又
,又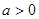
∴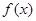 的值域为
的值域为 ,根据题设条件
,根据题设条件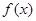 值域为
值域为 ,
,
故有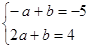 ,解得
,解得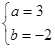 ,所以所求
,所以所求 、
、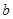 的值分别为3,
的值分别为3,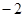 。
。
(Ⅱ)由(1)得 ,∴
,∴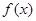 的最小正周期为
的最小正周期为 。
。
(Ⅲ)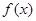 的单调减区间即为函数
的单调减区间即为函数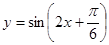 的单调增区间,
的单调增区间,
由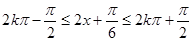 ,得
,得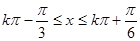
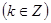 ,
,
故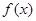 的单调减区间为
的单调减区间为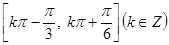 .
.
考点:三角函数的最值三角函数的周期性及求法
点评:本题考查的知识点是三角函数的最值,三角函数的周期性及其求法,其中根据降幂公式(逆用二倍角公式)及辅助角公式,我将函数解析式化为正弦型函数的形式,是解答本题的关键.

练习册系列答案
相关题目
 的一段图象如图所示.
的一段图象如图所示.
 的解析式;
的解析式; 个单位,得到
个单位,得到 的图象,求直线
的图象,求直线 与函数
与函数 的图象在
的图象在 内所有交点的坐标.
内所有交点的坐标. 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,向量
,向量 ,
, ,且
,且 .
. ,
, ,求
,求 .
. 的最小正周期;
的最小正周期; 的集合.
的集合. ,D为海岸线l上的一点.设CD=xkm(x>
,D为海岸线l上的一点.设CD=xkm(x> ),点D对跑道AB的视角为
),点D对跑道AB的视角为 .
.
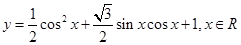
 取得最大值时,求自变量
取得最大值时,求自变量 的取值集合;
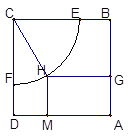
的取值集合;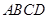 是一块边长为50m的正方形地皮,扇形
是一块边长为50m的正方形地皮,扇形 是运动场的一部分,其半径为40m,矩形
是运动场的一部分,其半径为40m,矩形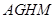 就是拟建的健身室,其中
就是拟建的健身室,其中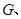
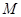 分别在
分别在 和
和 上,
上,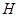 在弧
在弧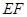 上,设矩形
上,设矩形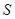 ,∠
,∠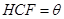 .
.
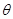 的函数;
的函数; ,求下列各式的值:
,求下列各式的值: ; (2)
; (2)  .
. ,
,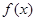 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程; 上的值域。
上的值域。