题目内容
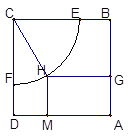
在申办国家级示范性高中期间,某校拟用运动场的边角地建一个矩形的健身室. 如图所示,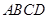 是一块边长为50m的正方形地皮,扇形
是一块边长为50m的正方形地皮,扇形 是运动场的一部分,其半径为40m,矩形
是运动场的一部分,其半径为40m,矩形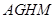 就是拟建的健身室,其中
就是拟建的健身室,其中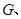
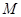 分别在
分别在 和
和 上,
上,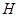 在弧
在弧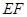 上,设矩形
上,设矩形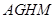 的面积为
的面积为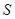 ,∠
,∠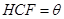 .
.
(1) 试将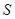 表示为
表示为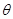 的函数;
的函数;
(2) 当点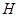 在弧
在弧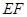 的何处时,该健身室的面积最大?最大面积为多少?
的何处时,该健身室的面积最大?最大面积为多少?
(1)
 .
.
(2)当点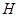 在弧
在弧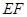 的端点
的端点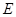 或
或 处时,健身室的面积最大,最大面积为500m2
处时,健身室的面积最大,最大面积为500m2
解析试题分析:解: (1) 延长 交
交 于
于 ,
, ∥
∥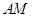 ,∴
,∴ .
. ,
,
∴ ,
, ,
,
于是 ,
, 4分
4分
∴矩形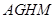 的面积为
的面积为
 . 6分
. 6分
(2)  .
.
设 ,则
,则 , 7分
, 7分 . 8分
. 8分 ,∴
,∴ . 10分
. 10分
∴当 时,
时,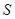 有最大值,且
有最大值,且 ,
,
此时, ,即
,即 ,
, ,∴
,∴ .
.
答:当点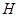 在弧
在弧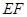 的端点
的端点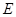 或
或 处时,健身室的面积最大,最大面积为500m2 . 12分
处时,健身室的面积最大,最大面积为500m2 . 12分
考点:三角函数的运用
点评:主要是考查了运用三角函数表示面积,以及求解最值的运用,属于中档题。

练习册系列答案
相关题目

 的最小正周期为
的最小正周期为 .
. 的值;
的值; 在区间
在区间 上的单调性.
上的单调性. (其中
(其中 >0),且函数
>0),且函数 的最小正周期为
的最小正周期为 .
. 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.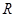 的函数
的函数
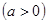 在区间
在区间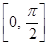 上的值域为
上的值域为 ,
, 、
、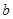 的值;
的值;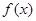 的最小正周期;
的最小正周期;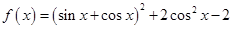 .
. 的最小正周期;
的最小正周期;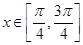 时,求函数
时,求函数 ,计算:
,计算: (2)
(2)
 ,
, ,函数
,函数 .
. 的最小正周期;(Ⅱ)若
的最小正周期;(Ⅱ)若 ,求函数
,求函数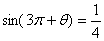 ,
, 的值;
的值;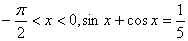 ,求
,求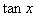 的值。
的值。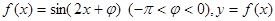 图像的一条对称轴是直线
图像的一条对称轴是直线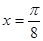 .
.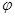 ;(2)画出函数
;(2)画出函数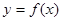 在区间
在区间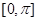 上的图像(在答题纸上完成列表并作图).
上的图像(在答题纸上完成列表并作图).