题目内容
设函数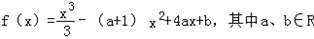
(Ⅰ)若函数f(x)在x=3处取得极小值是 ,求a、b的值;
,求a、b的值;
(Ⅱ)求函数f(x)的单调递增区间;
(Ⅲ)若函数f(x)在(﹣1,1)上有且只有一个极值点,求实数a的取值范围.
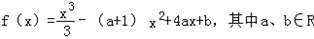
(Ⅰ)若函数f(x)在x=3处取得极小值是
 ,求a、b的值;
,求a、b的值;(Ⅱ)求函数f(x)的单调递增区间;
(Ⅲ)若函数f(x)在(﹣1,1)上有且只有一个极值点,求实数a的取值范围.
解:(I)∵f'(x)=x2﹣2(a+1)x+4a
∴f'(3)=9﹣6(a+1)+4a=0得 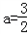
∵ 解得:b=﹣4
解得:b=﹣4
(II)∵f'(x)=x2﹣2(a+1)x+4a=(x﹣2a)(x﹣2)
令f'(x)=0,即x=2a或x=2.
当a>1时,2a>2,
∴f'(x)>0时,x>2a或x<2,即f(x)的单调递增区间为(﹣∞,2)和(2a,+∞).
当a=1时,f'(x)=(x﹣2)2≥0,即f(x)的单调递增区间为(﹣∞,+∞).
当a<1时,2a<2,∴f'(x)>0时,x<2a或x>2,
即f(x)的单调递增区间为(﹣∞,2a)和(2,+∞).
(Ⅲ)由题意可得: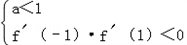
∴(2a﹣1)(2a+1)<0
∴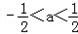
∴a的取值范围

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目