题目内容
2.已知等差数列{an}的前n项和为Sn,且a2=18-a7,S8=( )| A. | 18 | B. | 36 | C. | 54 | D. | 72 |
分析 由等差数列{an}的性质可得:a1+a8=a2+a7.再利用前n项和公式即可得出.
解答 解:由等差数列{an}的性质可得:a1+a8=a2+a7.
∴S8=$\frac{8({a}_{1}+{a}_{8})}{2}$=4×18=72.
故选:D.
点评 本题考查了等差数列的性质、前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
13.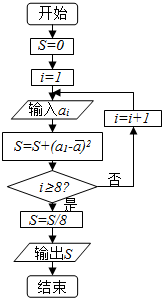 对一名学生数学成绩统计了8次,第i次统计得到的数据为ai,具体如下表所示:
对一名学生数学成绩统计了8次,第i次统计得到的数据为ai,具体如下表所示:
在对上述统计数据的分析中,一部分计算见如图所示的算法流程图(其中$\overline{a}$是这8个数据的平均数),则输出的S的值是( )
 对一名学生数学成绩统计了8次,第i次统计得到的数据为ai,具体如下表所示:
对一名学生数学成绩统计了8次,第i次统计得到的数据为ai,具体如下表所示:| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ai | 100 | 101 | 103 | 103 | 104 | 106 | 107 | 108 |
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
10.函数y=(a-2)x在R上为增函数,则a的取值范围是( )
| A. | a>3 | B. | a>0且a≠1 | C. | a<3 | D. | 2<a<3 |
14.已知数列{an}中,满足an+1-an-3=0,则数列{an}是( )
| A. | 递增数列 | B. | 递减数列 | C. | 摆动数列 | D. | 常数列 |
12.设集合A={$\frac{n}{2}$|n∈Z},B={n|n∈Z},C={n+$\frac{1}{2}$|n∈Z},D={$\frac{n}{3}$+$\frac{1}{6}$|n∈Z},则在下列关系式中,成立的是( )
| A. | A$\underset{?}{≠}$B$\underset{?}{≠}$C$\underset{?}{≠}$D | B. | A∩B=∅,C∩D=∅ | C. | A=B∪C,C$\underset{?}{≠}$D | D. | A∪B=B ,C∩D=∅ |
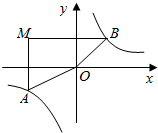 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.
如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.