题目内容
19.如图,在斜三棱柱![]() ,侧面
,侧面![]() 与底面ABC所成的二面角为120°,E、F分别是棱
与底面ABC所成的二面角为120°,E、F分别是棱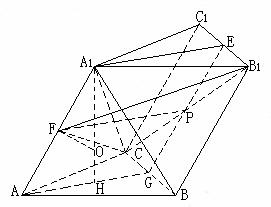 的中点.
的中点.
(Ⅰ)求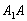 与底面ABC所成的角;
与底面ABC所成的角;
(Ⅱ)证明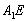 //平面
//平面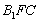 ;
;
(Ⅲ)求经过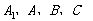 四点的球的体积.
四点的球的体积.
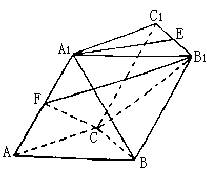
19.(Ⅰ)解:过A1作A1H⊥平面ABC,垂足为H.
连结AH,并延长交BC于G,连结EG,于是∠A1AH为A1A与底面ABC所成的角
 ∵∠A1AB=∠A1AC
∵∠A1AB=∠A1AC
∴AG为∠BAC的平分线。
又∵AB=AC,∴AG⊥BC,且G为BC的中点因此,由三垂线定理,A1A⊥BC
∵A1A∥B1B,且EC∥B1B EC⊥BC,于是∠AGE为二面角A-BC-E的平面角,即
∠AGE=120°
由于四边形A1AGE为平行四边形,得
∠A1AG=60°
所以,A1A与底面ABC所成的角为60°。
(Ⅱ)证明:设EG与B1C的交点为P,则点P为EG的中点,连结PF。
在平行四边形AGEA1中,因F为A1A的中点,故A1E∥FP.
而FP![]() 平面B1FC,A1E
平面B1FC,A1E![]() 平面B1FC,所以A1E∥平面B1FC.
平面B1FC,所以A1E∥平面B1FC.
(Ⅲ)解:连结A1C,在△A1AC和△A1AB中,由于AC=AB, ∠A1AC=∠A1AB,A1A= A1A,则△A1AC≌△A1AB,故A1C=A1B.由已知得
A1A= A1B=A1C=a
又∵A1H⊥平面ABC,∴H为BC的外心.
设所求球的球心为O,则O∈A1H,且球心O与A1A中点的连线OF⊥A1A.
在Rt△A1FO中,
A1O=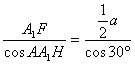 =
=![]() 。
。
故所求球的半径R=![]() a. 球的体积
a. 球的体积
V=![]() πR3=
πR3=![]() π(
π(![]() a)3=
a)3=![]() πa3。
πa3。

练习册系列答案
相关题目

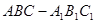 中,点
中,点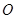 、
、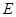 分别是
分别是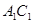 、
、 的中点,
的中点,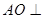 平面
平面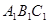 .已知
.已知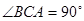 ,
, .
.
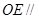 平面
平面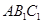 ;
;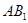 与
与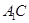 所成的角;
所成的角;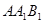 所成角的正弦值.
所成角的正弦值.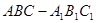 中,
中, ,又
,又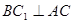 ,过
,过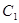 作
作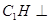 底面
底面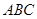 ,垂足为
,垂足为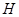 ,则点
,则点
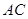 上
B.直线
上
B.直线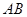 上
上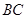 上
D.
上
D.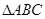 的内部
的内部
 (Ⅰ)证明:
(Ⅰ)证明: