题目内容
(本小题满分14分)已知函数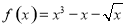
(1)判断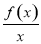 的单调性;
的单调性;
(2)求函数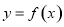 的零点的个数;
的零点的个数;
(3)令 ,若函数
,若函数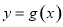 在
在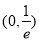 内有极值,求实数
内有极值,求实数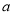 的取值范围。
的取值范围。
(1)(0,+∞)上单调递增;(2)两个;(3)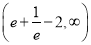
【解析】
试题分析:(1)设φ(x)=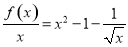 ,其中(x>0),
,其中(x>0),
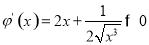
∴φ(x)在(0,+∞)上单调递增
(2)∵φ(1)=-1<0,φ(2)=3-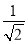 >0,有φ(x)在(0,+∞)上单调递增,
>0,有φ(x)在(0,+∞)上单调递增,
故φ(x)在(1,2)内有唯一零点,显然x=0为f(x)的一个零点
又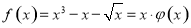 ,显然x=0为f(x)的一个零点,
,显然x=0为f(x)的一个零点,
因此y=f(x)在(0,+∞)有且仅有两个零点
(3)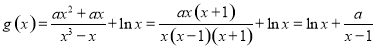 ,
,
则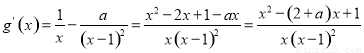 ,
,
设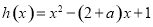 ,则h(x)=0有两个不同的根
,则h(x)=0有两个不同的根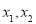 ,且有一根在
,且有一根在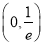 内,
内,
不妨设, 由于
由于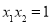 ,所以
,所以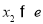 ,
,
由于h(0)=1,故只需h(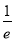 )<0即可,即
)<0即可,即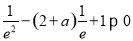 ,
,
解得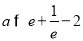 .
.
考点:利用导数研究函数的单调性,极值,闭区间上的最值

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 与直线
与直线 互相垂直,那么
互相垂直,那么 的值等于 ( )
的值等于 ( ) C.
C. D.
D.
 是
是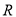 上的奇函数,且在区间
上的奇函数,且在区间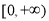 上单调递增,若
上单调递增,若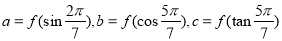 ,则 ( )
,则 ( )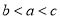 B.
B.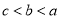 C.
C.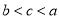 D.
D.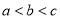
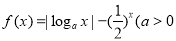 且
且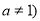 有两个零点
有两个零点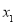 、
、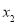 ,则有( )
,则有( )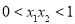 (B)
(B)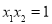 (C)
(C)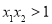 (D)
(D)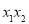 的范围不确定
的范围不确定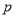 且
且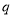 ”为假,则
”为假,则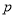 、
、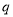 至少有一个是假命题
至少有一个是假命题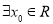 ,
,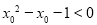 ”的否定是“
”的否定是“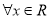 ,
,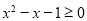 ”
”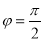 ”是“
”是“ 为偶函数”的充要条件
为偶函数”的充要条件 时,幂函数
时,幂函数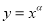 在
在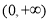 上单调递减
上单调递减 中,直线
中,直线 是曲线
是曲线 的切线,则当
的切线,则当 时,实数
时,实数 的最小值是
的最小值是 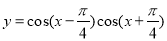 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为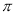 ;
; 且
且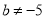 ”是“
”是“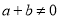 ”的必要不充分条件;
”的必要不充分条件;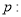 对任意的
对任意的 ,都有
,都有 ,则“
,则“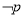 是:存在
是:存在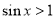 ”;
”;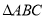 中,若
中,若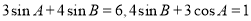 ,则角
,则角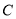 等于
等于 或
或 。
。 =
= ,若对
,若对
 ,
, ∈(0,1),且
∈(0,1),且 ,都有
,都有 为真命题,则实数
为真命题,则实数 的取值范围 .
的取值范围 .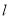 经过直线
经过直线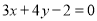 与直线
与直线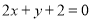 的交点
的交点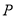 , 且垂直于直线
, 且垂直于直线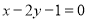 .
.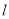 与两坐标轴围成的三角形的面积
与两坐标轴围成的三角形的面积 .
.