题目内容
(本题满分12分) 已知直线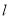 经过直线
经过直线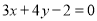 与直线
与直线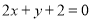 的交点
的交点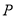 , 且垂直于直线
, 且垂直于直线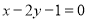 .
.
(1)求直线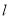 的方程;
的方程;
(2)求直线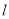 与两坐标轴围成的三角形的面积
与两坐标轴围成的三角形的面积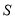 .
.
(1)y=-2x-2(也可以写成2x+y+2=0);(2)1
【解析】
试题分析:由已知 ,可得
,可得 ,交点P(-2,2)
,交点P(-2,2)
又因为所求直线垂直于直线x-2y-1=0,可得所求的直线的斜率k=-2
故直线方程为y-2=-2(x+2),即y=-2x-2(也可以写成2x+y+2=0)
(2)令x=0,可得y=-2;令y=0,可得x=-1
所以
考点:本题考查求直线方程,直线与直线的位置关系
点评:解决本题的关键是掌握两直线垂直的充要条件

练习册系列答案
相关题目
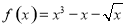
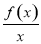 的单调性;
的单调性;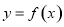 的零点的个数;
的零点的个数; ,若函数
,若函数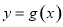 在
在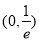 内有极值,求实数
内有极值,求实数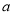 的取值范围。
的取值范围。 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,腰和上底均为
,腰和上底均为 的等腰梯形,那么原平面图形的面积是( )
的等腰梯形,那么原平面图形的面积是( ) B.
B. C、
C、  D.
D.
 ”是“
”是“ ”的( )
”的( ) 与
与 的距离为 ___________________
的距离为 ___________________  轴截得的弦长等于( )
轴截得的弦长等于( ) (D)1
(D)1 ,且
,且 ,若函数
,若函数 在区间
在区间 上的最大值为2,则
上的最大值为2,则 ( )
( ) B.
B. C.
C. D.
D.
 被圆
被圆 截得的弦长为__________.
截得的弦长为__________.