题目内容
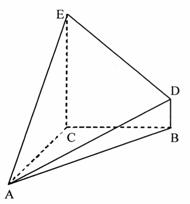
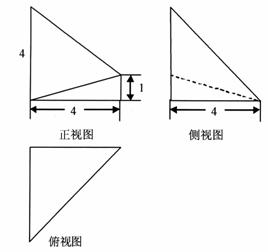
已知几何体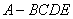 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(Ⅰ)求此几何体的体积;
(Ⅱ)求异面直线 与
与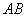 所成角的余弦值;
所成角的余弦值;
 (Ⅲ)探究在
(Ⅲ)探究在 上是否存在点Q,使得
上是否存在点Q,使得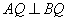 ,并说明理由.
,并说明理由.
解:(Ⅰ)由该几何体的三视图可知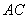 垂直于底面
垂直于底面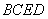 ,且
,且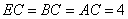 ,
, ,
,

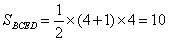 ,
,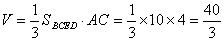 ,此几何体的体积为
,此几何体的体积为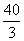 ;
;
解法一:(Ⅱ)过点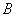 作
作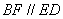 交
交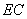 于
于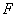 ,连接
,连接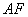 ,则
,则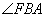 或其补角即为异面直线
或其补角即为异面直线 与
与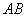 所成角,在
所成角,在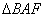 中,
中,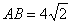 ,
,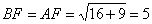 ,
,

 ;即异面直线
;即异面直线 与
与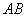 所成角的余弦值为
所成角的余弦值为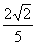 。
。
 (Ⅲ)在
(Ⅲ)在 上存在点Q,使得
上存在点Q,使得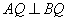 ;取
;取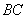 中点
中点 ,过点
,过点 作
作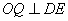 于点
于点 ,则点
,则点 为所求点;连接
为所求点;连接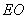 、
、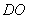 ,在
,在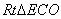 和
和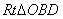 中,
中,

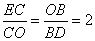 ,
,
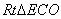 ∽
∽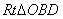 ,
,
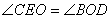 ,
,

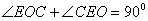 ,
,
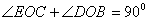 ,
,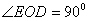 ,
,

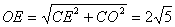 ,
,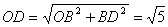 ,
,
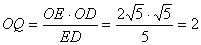 ,
,
 以
以 为圆心,
为圆心,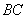 为直径的圆与
为直径的圆与 相切,切点为
相切,切点为 ,连接
,连接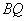 、
、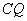 ,可得
,可得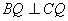 ;
;

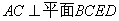 ,
,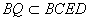 ,
,
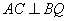 ,
,
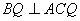 ,
,

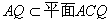 ,
,
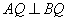 ;
;
解法二:(Ⅰ)同上。
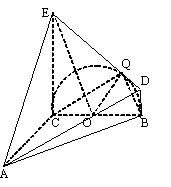
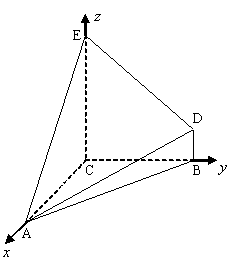 (Ⅱ)以
(Ⅱ)以 为原点,以
为原点,以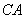 、
、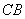 、
、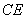 所在直线为
所在直线为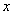 、
、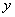 、
、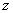 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则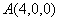 ,
,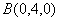 ,
,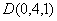 ,
,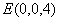 ,得
,得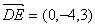 ,
,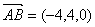 ,
,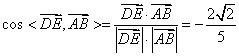 ,又异面直线
,又异面直线 与
与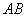 所成角为锐角,异面直线
所成角为锐角,异面直线 与
与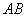 所成角的余弦值为
所成角的余弦值为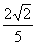 。
。
(Ⅲ)设存在满足题设的点 ,其坐标为
,其坐标为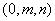 ,
,
则 ,
,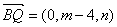 ,
,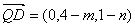 ,
,

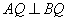 ,
,
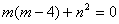 ①;
①;
 点
点 在
在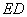 上,
上, 存在
存在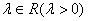 使得
使得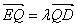 ,
,
即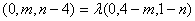 ,化简得
,化简得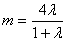 ,
,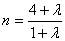 ②,
②,
②代入①得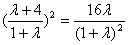 ,得
,得 ,
,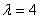 ;
;
 满足题设的点
满足题设的点 存在,其坐标为
存在,其坐标为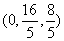 。
。

练习册系列答案
相关题目
 则
则 .
. A .
A . 



 中,底面
中,底面 为矩形,
为矩形, 平面
平面 在线段
在线段 上,
上, 平面
平面 .
. 平面
平面 ;
; ,
, ,求二面角
,求二面角 的正切值.
的正切值.
 的三个内角满足
的三个内角满足 ,则△
,则△
 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为 、
、 、
、 ,已知
,已知 ,且
,且 求b
求b 

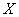 ,则
,则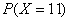 的值为( )
的值为( )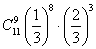 B.
B. 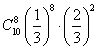 C.
C.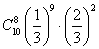 D.
D.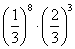
 B.
B. C.
C. D.
D.