题目内容
如图5所示,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 平面
平面 ,点
,点 在线段
在线段 上,
上, 平面
平面 .
.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)若 ,
, ,求二面角
,求二面角 的正切值.
的正切值.

 解析:(Ⅰ)因为
解析:(Ⅰ)因为 平面
平面 ,
, 平面
平面 ,所以
,所以 .又因为
.又因为 平面
平面 ,
, 平面
平面 ,所以
,所以 .而
.而 ,
, 平面
平面 ,
, 平面
平面 ,所以
,所以 平面
平面 .
.
(Ⅱ)由(Ⅰ)可知 平面
平面 ,而
,而 平面
平面 ,所以
,所以 ,而
,而 为矩形,所以
为矩形,所以 为正方形,于是
为正方形,于是 .
.
 法1:以
法1:以 点为原点,
点为原点, 、
、 、
、 为
为 轴、
轴、 轴、
轴、 轴,建立空间直角坐标系
轴,建立空间直角坐标系 .则
.则 、
、 、
、 、
、 ,于是
,于是 ,
, .设平面
.设平面 的一个法向量为
的一个法向量为
 ,则
,则 ,从而
,从而 ,令
,令 ,得
,得 .而平面
.而平面 的一个法向量为
的一个法向量为
 .所以二面角
.所以二面角 的余弦值为
的余弦值为 ,于是二面角
,于是二面角
 的正切值为3.
的正切值为3.
法2:设 与
与 交于点
交于点 ,连接
,连接 .因为
.因为 平面
平面 ,
, 平面
平面 ,
, 平面
平面 ,所以
,所以 ,
, ,于是
,于是 就是二面角
就是二面角 的平面角.又因为
的平面角.又因为 平面
平面 ,
, 平面
平面 ,所以
,所以 是直角三角形.由
是直角三角形.由 ∽
∽ 可得
可得 ,而
,而 ,所以
,所以 ,
, ,而
,而 ,所以
,所以 ,于是
,于是 ,而
,而 ,于是二面角
,于是二面角 的正切值为
的正切值为 .
.


练习册系列答案
相关题目
“单独二胎”政策的落实是我国完善计划生育基本国策的一项重要措施,事先需要做大量的调研论证.现为了解我市市民对该项措施是否认同,拟从全体市民中抽取部分样本进行调查.调查结果如下表:
| 调查人数 | 2 | 10 | 70 | 130 | 310 | 700 | 1500 | 2000 | 3000 | 5000 |
| 认同人数 | 2 | 9 | 60 | 116 | 286 | 639 | 1339 | 1810 | 2097 | 4515 |
| 认同频率 | 1 | 0.9 | 0.857 | 0.892 | 0.922 | 0.913 | 0.893 | 0.905 | 0.899 | 0.903 |
则根据上表我们可以推断市民认同该项措施的概率最有可能为 ( )
A.0.80 B.0.85 C.0.90 D.0.92

 的值;
的值; 的值;
的值; 是第三象限角,求
是第三象限角,求 的值.
的值. B.
B. C.
C. D.
D.

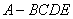 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形. 与
与 所成角的余弦值;
所成角的余弦值;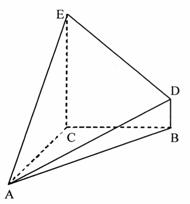 (Ⅲ)探究在
(Ⅲ)探究在 ,并说明理由.
,并说明理由.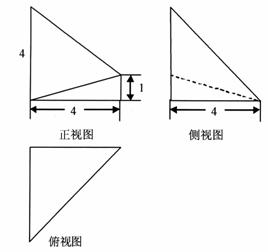
 ,
, ,则A=
,则A= (B)
(B) (C)
(C) (D)
(D)

 的解集不是空集,求实数a的取值范围;
的解集不是空集,求实数a的取值范围; 有实根,求实数m的取值范围。
有实根,求实数m的取值范围。