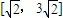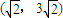题目内容
已知m,n是夹角为60°的两个单位向量,求a=2m+n和b=(-3m+2n)的夹角.
解:|a|2=4|m|2+4m·n+|n|2=7,
即|a|=![]() ,同理,|b|=
,同理,|b|=![]() .
.
a·b=-![]() ,
,
cos〈a,b〉=a·b|a||b|=-![]() ,
,
又∵0≤〈a,b〉≤π,
∴〈a,b〉=![]() .
.

练习册系列答案
相关题目
已知向量
=(m-1,n-1),
=(m-3,n-3)且
与
的夹角为钝角,则m+n的取值范围是( )
| a |
| b |
| a |
| b |
| A、[2,6] | ||||
B、[
| ||||
C、(
| ||||
| D、(2,6) |
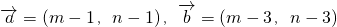 且
且 与
与 的夹角为钝角,则m+n的取值范围是
的夹角为钝角,则m+n的取值范围是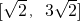
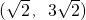
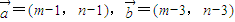 且
且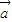 与
与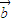 的夹角为钝角,则m+n的取值范围是( )
的夹角为钝角,则m+n的取值范围是( )