题目内容
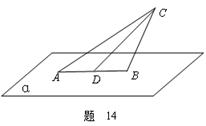
如图,已知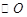 的直径AB=3,点C为
的直径AB=3,点C为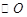 上异于A,B的一点,
上异于A,B的一点,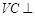 平面ABC,且VC=2,点M为线段VB的中点.
平面ABC,且VC=2,点M为线段VB的中点.
(1)求证: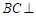 平面VAC;
平面VAC;
(2)若AC=1,求直线AM与平面VAC所成角的大小.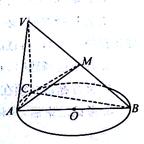
(1)略;(2)
解析试题分析:(1)证明直线与平面垂直的关键是证明该直线与平面内两条相交直线都垂直;(2)求直线与平面所成角的关键是找出直线在平面内的射影,进而构造直角三角形,求出线面角.
试题解析:(1)∵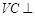 平面
平面 ,
, 平面
平面
∴ 2分
2分
∵点C为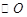 上一点,且AB为直径
上一点,且AB为直径
∴ 4分
4分
又 平面VAC,
平面VAC,
∴ 平面VAC; 6分
平面VAC; 6分
(2)如图,取VC的中点N,连接MN,AN,则MN∥BC
由(1)得,BC⊥平面VAC
∴MN⊥平面VAC
∴∠MAN为直线AM与平面VAC所成的角 9分
∵

∴
∴
∴直线AM与平面VAC所成角的大小为 12分
12分
考点:空间直线与平面垂直的判定,直线与平面所成角及其计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
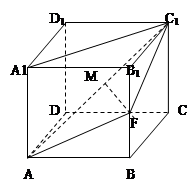
 中,
中,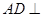 平面
平面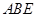 ,
,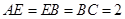 ,
, 为
为 上的点,
上的点, 平面
平面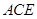
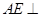 平面
平面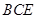 ;
;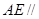 平面
平面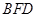 ;
;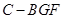 的体积。
的体积。
 中,
中, ,
, 分别是
分别是 的中点,且
的中点,且
 .
.
 与
与 所成角的大小;
所成角的大小; 与平面
与平面 所成角的正弦值.
所成角的正弦值. 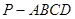 的底面为菱形,
的底面为菱形,
 面
面 ,且
,且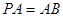 ,
,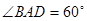 ,
,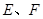 分别是
分别是 的中点.
的中点.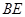 ∥平面
∥平面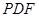 ;
;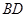 作一平面交棱
作一平面交棱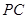 于点
于点 ,若二面角
,若二面角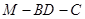 的大小为
的大小为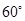 ,求
,求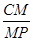 的值.
的值.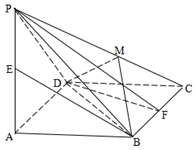
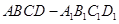 中,
中,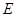 是
是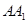 的中点.
的中点.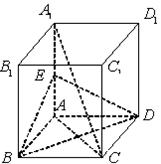
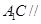 平面
平面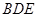 ;
;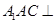 平面
平面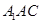 所成角的正弦值.
所成角的正弦值. 中,点
中,点 在边
在边 上,
上,

 平面
平面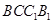 ;
; 是
是 的中点,求证:
的中点,求证: //平面
//平面 .
.
 中,AB=9,AC=15,
中,AB=9,AC=15, ,平面ABC外一点P到三个顶点A、B、C的距离均为14,则P到平面ABC的距离为 。
,平面ABC外一点P到三个顶点A、B、C的距离均为14,则P到平面ABC的距离为 。
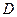 为
为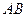 的中点,
的中点,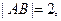
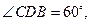
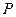 为
为 内的动点,且
内的动点,且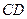 的距离为
的距离为 则
则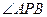 的最大值为________________.
的最大值为________________.