题目内容
设定义在[－2,2]上的偶函数f(x)在区间[－2,0]上单调递减，若f(1－m)<f(m)，求实数m的取值范围．
由偶函数性质知f(x)在[0,2]上单调递增，且f(1－m)＝f(|1－m|)，f(m)＝f(|m|)，
因此f(1－m)<f(m)等价于
解得：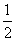
<m≤2.
因此实数m的取值范围是(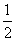，2]．
练习册系列答案
相关题目
题目内容
设定义在[－2,2]上的偶函数f(x)在区间[－2,0]上单调递减，若f(1－m)<f(m)，求实数m的取值范围．
由偶函数性质知f(x)在[0,2]上单调递增，且f(1－m)＝f(|1－m|)，f(m)＝f(|m|)，
因此f(1－m)<f(m)等价于
解得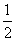：<m≤2.
因此实数m的取值范围是(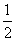，2]．
在区间[1,2]上都是减函数，则a的取值范围是________．
<0的解集是________．
3)，c＝f(0.20.6)，则a、b、c的大小关系是( )