题目内容
类比平面内 “垂直于同一条直线的两条直线互相平行”的性质,可推出空间下列结论:
①垂直于同一条直线的两条直线互相平行 ②垂直于同一个平面的两条直线互相平行
③垂直于同一条直线的两个平面互相平行 ④垂直于同一个平面的两个平面互相平行
则正确的结论是 ( )
| A.①② | B.②③ | C.③④ | D.①④ |
B
解析试题分析:②③正确,因为①中两直线还可能相交或异面,④中两平面还有可能相交。故B正确。
考点:1空间两直线的位置关系;2空间两平面的位置关系。

练习册系列答案
相关题目
设 ,b,c是空间三条不同的直线,
,b,c是空间三条不同的直线, ,
, 是空间两个不同的平面,则下列命题不成立的是( )
是空间两个不同的平面,则下列命题不成立的是( )
A.当 时,若 时,若 ⊥ ⊥ ,则 ,则 ∥ ∥ |
B.当 ,且 ,且 是 是 在 在 内的射影时,若b⊥c,则 内的射影时,若b⊥c,则 ⊥b ⊥b |
C.当 时,若b⊥ 时,若b⊥ ,则 ,则 |
D.当 时,若c∥ 时,若c∥ ,则b∥c ,则b∥c |
下列命题正确的是( )
| A.若两条直线和同一个平面所成的角相等,则这两条直线平行 |
| B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行 |
| C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行 |
| D.若两个平面都垂直于第三个平面,则这两个平面平行 |
设 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,给出下列条件,能得到
是两个不同的平面,给出下列条件,能得到 的是( )
的是( )
A. | B. | C. | D. |
若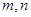 是两条不同的直线,
是两条不同的直线,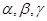 是三个不同的平面,则下列命题中正确命题是( )
是三个不同的平面,则下列命题中正确命题是( )
A.若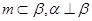 ,则 ,则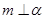 |
B.若 , ,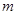 ∥ ∥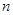 ,则 ,则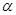 ∥ ∥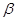 |
C.若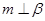 , ,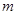 ∥ ∥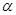 ,则 ,则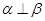 |
D.若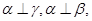 则 则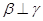 |
设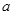 、
、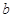 是两条不同的直线,
是两条不同的直线,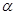 、
、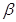 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )
A.若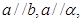 则 则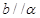 | B.若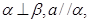 则 则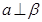 |
C.若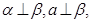 则 则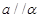 | D.若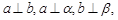 则 则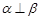 |
已知两条直线y=ax﹣2和3x﹣(a+2)y+1=0互相平行,则a等于( )
| A.1或﹣3 | B.﹣1或3 | C.1或3 | D.﹣1或﹣3 |
对于直线m,n和平面α,β,α⊥β的一个充分条件是( )
| A.m⊥n,m∥α,n∥β | B.m⊥n,α∩β=m,n?α |
| C.m∥n,n⊥β,m?α | D.m∥n,m⊥α,n⊥β |
 是两条不重合的直线,
是两条不重合的直线, 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: ,
, ,且
,且 ,则
,则 ;
; ,且
,且 ,
, ,则
,则 ;
;