题目内容

如图11，已知在△ABC中，∠BAC=90°，AD⊥BC，E是AC的中点，ED交AB的延长线于F.求证：.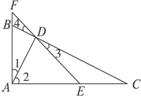

           图11

思路分析:比例式左边AB、AC在△ABC中，右边DF、AF在△ADF中，这两个三角形不相似，因此本题需经过中间比进行代换.通过证明两套三角形分别相似证得结论.

证明:∵∠BAC=90°，AD⊥BC，

∴∠ADB=∠ADC=∠BAC=90°.

∴∠1＋∠2=90°，∠2＋∠C=90°.

∴∠1=∠C.∴△ABD∽△CAD.

∴.

又∵E是AC中点，∴DE=EC.∴∠3=∠C.

又∵∠3=∠4，∠1=∠C，∴∠1=∠4.又有∠F=∠F，∴△FBD∽△FDA.

∴.

练习册系列答案
相关题目
精英家教网2009年11月30时3时许，位于哈尔滨市南岗区东大直街323号的大世界商城发生火灾，为扑灭某着火点，现场安排了两支水枪，如图，D是着火点，A，B分别是水枪位置，已知AB=15
2
米，在A处看到着火点的仰角为60°，∠ABC=30°，∠BAC=105°，求两支水枪的喷射距离至少是多少？
已知函数g（x）=Asin（wx+φ）（A＞0，w＞0，0＜φ＜π）的图象如图所示，其中点A（
π
3
，2）、B（
11π
6
，0）分别是函数的最大值点和零点．
（I）求函数y=g（x）的解析式；
（Ⅱ）若函数f（x）=2g（x）cosx+m在[0，
π
2
]上的最大值为6，求函数f（x）在R上的最小值及相应的x值的集合．
[选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．
A．（选修4-1：几何证明选讲）
如图，圆O的直径AB=8，C为圆周上一点，BC=4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，求线段AE的长．
B．（选修4-2：矩阵与变换）
已知二阶矩阵A有特征值λ1=3及其对应的一个特征向量α1=
1
1
，特征值λ2=-1及其对应的一个特征向量α2=
1
-1
，求矩阵A的逆矩阵A-1．
C．（选修4-4：坐标系与参数方程）
以平面直角坐标系的原点O为极点，x轴的正半轴为极轴，建立极坐标系（两种坐标系中取相同的单位长度），已知点A的直角坐标为（-2，6），点B的极坐标为(4，
π
2
)，直线l过点A且倾斜角为
π
4
，圆C以点B为圆心，4为半径，试求直线l的参数方程和圆C的极坐标方程．
D．（选修4-5：不等式选讲）
设a，b，c，d都是正数，且x=
a2+b2
，y=
c2+d2
．求证：xy≥
(ac+bd)(ad+bc)
．
如图，已知点A（11，0），函数y=
x+1
的图象上的动点P在x轴上的射影为H，且点H在点A的左侧．设|PH|=t，△APH的面积为f（t）．
（Ⅰ）求函数f（t）的解析式及t的取值范围；
（Ⅱ）求函数f（t）的最大值．
精英家教网已知函数f（x）=
2
sin（ωx+
π
4
）在一个周期内的图象如图所示，且在△ABC中，AB=AC=
11
，则ω=（　　）
A、
π
3
B、
π
6
C、
π
4
D、π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网