题目内容
 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60,
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60,(1)求点A到平面PBD的距离的值;
(2)求二面角A-PB-D的余弦值.
分析:(1)点A到面PBD的距离可以转化成向量DA在面PBD的法向量量上的投影的长度来求解;
(2)二面角A-PB-D的余弦值可以转化成求平面PAB与平面PBD的法向量夹角的余弦值问题来解决,求出两个平面的法向量,用数量积公式求两个向量夹角的余弦值,此余弦值与二面角的余弦值的关系是绝对值相等,从图可以看出所求二面角的余弦值为正,故可求.
(2)二面角A-PB-D的余弦值可以转化成求平面PAB与平面PBD的法向量夹角的余弦值问题来解决,求出两个平面的法向量,用数量积公式求两个向量夹角的余弦值,此余弦值与二面角的余弦值的关系是绝对值相等,从图可以看出所求二面角的余弦值为正,故可求.
解答: 解:由题意,连接AC,BD交于点O,由于四边形ABCD是菱形可得AC,BD互相垂直,以OA、OB所在直线分别x轴,y轴,以过O且垂直平面ABCD的直线为z轴,建立空间直角坐标系,则A(
解:由题意,连接AC,BD交于点O,由于四边形ABCD是菱形可得AC,BD互相垂直,以OA、OB所在直线分别x轴,y轴,以过O且垂直平面ABCD的直线为z轴,建立空间直角坐标系,则A(
,0,0),B(0,1,0),C(-
,0,0),D(0,-1,0),P(
,0,2),
=(0,2,0),
=(0,0,2)(2分)
(Ⅰ)设平面PDB的法向量为
=(x1 ,y1,z1),
=(
,1,2),
=(0,2,0)
由
,得
,令z1=1, 得
=(-
,0,1),
=(
,1,0)
所以点A到平面PDB的距离d=
=
(5分)
(Ⅱ)设平面ABP的法向量
=(x2,y2,z2),
=(0,0,2).
=(-
,1,0),
由
,得
=0,令y2=1,得
,∴
=(
,1,0),
∴cos<
,
>=
=-
,而所求的二面角与<
,
>互补,
所以二面角A-PB-D的余弦值为
 解:由题意,连接AC,BD交于点O,由于四边形ABCD是菱形可得AC,BD互相垂直,以OA、OB所在直线分别x轴,y轴,以过O且垂直平面ABCD的直线为z轴,建立空间直角坐标系,则A(
解:由题意,连接AC,BD交于点O,由于四边形ABCD是菱形可得AC,BD互相垂直,以OA、OB所在直线分别x轴,y轴,以过O且垂直平面ABCD的直线为z轴,建立空间直角坐标系,则A(| 3 |
| 3 |
| 3 |
| DB |
| AP |
(Ⅰ)设平面PDB的法向量为
| n1 |
| DP |
| 3 |
| DB |
由
|
|
| n1 |
2
| ||
| 3 |
| DA |
| 3 |
所以点A到平面PDB的距离d=
|
| ||||
|
|
2
| ||
| 7 |
(Ⅱ)设平面ABP的法向量
| n2 |
| AP |
| AB |
| 3 |
由
|
|
|
,∴
| n2 |
| ||
| 3 |
∴cos<
| n1 |
| n2 |
| ||||
|
|
| ||
| 7 |
| n1 |
| n2 |
所以二面角A-PB-D的余弦值为
| ||
| 7 |
点评:本题考点是点、线、面间的距离计算,本题把求点到面距离的问题转化成了求投影长度的问题,把求二面角的问题转化成了求向量夹角的问题,体现了化归的思想,在立体几何中求距离与求夹角的问题常借助空间向量的知识来解决.用空间向量法求二面角的余弦值时,一定要注意法向量的方向,如此才能保证正确求出二面角的余弦值,若两法向量的方向都指向二面角的内部则法向量的余弦值就是二面角的余弦值,若全指向二面角的外部,此时二者亦相等,若一指向外部一指向内部,则二者互为相反数,求解时要注意判断二者的关系.

练习册系列答案
相关题目
 15、如图四边形ABCD是菱形,PA⊥平面ABCD,Q为PA的中点.
15、如图四边形ABCD是菱形,PA⊥平面ABCD,Q为PA的中点. 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.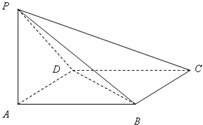 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.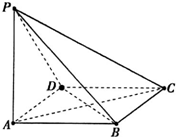 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.