题目内容
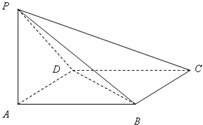 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.(1)求证:平面PBD⊥平面PAC;
(2)求点A到平面PBD的距离;
(3)求二面角B-PC-A的大小.
分析:(1)要证平面PBD⊥平面PAC,我们可以在一个平面内寻找另一平面的垂线,即证BD⊥平面PAC.利用线线垂直,可以证得线面垂直;
(2)先找出表示点A到平面PBD的距离的线段,AC∩BD=O,连接PO,过A作AE⊥PO交PO于E,所以AE⊥平面PBD,AE就是所求的距离,故可求;
(3)先利用三垂线定理,作出二面角B-PC-A的平面角,再利用三角形的相似即可求得.
(2)先找出表示点A到平面PBD的距离的线段,AC∩BD=O,连接PO,过A作AE⊥PO交PO于E,所以AE⊥平面PBD,AE就是所求的距离,故可求;
(3)先利用三垂线定理,作出二面角B-PC-A的平面角,再利用三角形的相似即可求得.
解答:证明:(1)∵ABCD为菱形,∴BD⊥AC
∵PA⊥平面ABCD,∴BD⊥PA
∵AC∩PA=A
∴BD⊥平面PAC
∵BD?平面PBD
∴平面PBD⊥平面PAC (3分)
(2)AC∩BD=O,连接PO,过A作AE⊥PO交PO于E,
∴AE⊥平面PBD,AE就是所求的距离,
在三角形PAO中,PA=2,AO=
,
∴PO=
,
∴AE=
=
.(3分)
(3)过O作OF⊥PC,连BF,
∵OB⊥平面PAC,由三垂线定理,PC⊥BF,
∴∠OFB为二面角B-PC-A的平面角,
∵AC=2
,PC=4,OC=
,Rt△OFC~Rt△PAC
∴
=
⇒
=
⇒OF=
∴tan∠OFB=
=
=
∴∠OFB=arctan
,所求二面角大小为arctan
(3分)
∵PA⊥平面ABCD,∴BD⊥PA
∵AC∩PA=A
∴BD⊥平面PAC
∵BD?平面PBD
∴平面PBD⊥平面PAC (3分)
(2)AC∩BD=O,连接PO,过A作AE⊥PO交PO于E,
∴AE⊥平面PBD,AE就是所求的距离,
在三角形PAO中,PA=2,AO=
| 3 |
∴PO=
| 7 |
∴AE=
| PA×AO |
| PO |
2
| ||
| 7 |
(3)过O作OF⊥PC,连BF,
∵OB⊥平面PAC,由三垂线定理,PC⊥BF,
∴∠OFB为二面角B-PC-A的平面角,
∵AC=2
| 3 |
| 3 |
∴
| OF |
| PA |
| OC |
| PC |
| OF |
| 2 |
| ||
| 4 |
| ||
| 2 |
∴tan∠OFB=
| OB |
| OF |
| 1 | ||||
|
2
| ||
| 3 |
∴∠OFB=arctan
2
| ||
| 3 |
2
| ||
| 3 |
点评:本题以线面垂直为载体,考查面面垂直,考查点面距离,考查面面角,解题的关键是正确运用面面垂直的判定定理,找出表示点面距离的线段及面面角.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60,
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60, 15、如图四边形ABCD是菱形,PA⊥平面ABCD,Q为PA的中点.
15、如图四边形ABCD是菱形,PA⊥平面ABCD,Q为PA的中点. 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.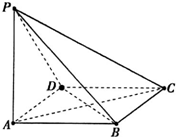 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.