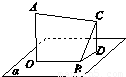
题目内容
 如图所示,AO⊥平面α,BC⊥OB,BC与平面α的夹角为30°,AO=BO=BC=a,则AC=
如图所示,AO⊥平面α,BC⊥OB,BC与平面α的夹角为30°,AO=BO=BC=a,则AC=| 2 |
| 2 |
分析:作CD⊥平面α,垂足为D,连接BD,OD,过C作CE⊥AO,垂足为E,求出CE=
a,AE=
a,即可求得结论.
| ||
| 2 |
| 1 |
| 2 |
解答:解:作CD⊥平面α,垂足为D,连接BD,OD,则∠CBD=30°,

∵BO=BC=a,∴OD=
a,CD=
a
过C作CE⊥AO,垂足为E,则CE=
a,AE=
a
∴AC=
=
a
故答案为:
a

∵BO=BC=a,∴OD=
| ||
| 2 |
| 1 |
| 2 |
过C作CE⊥AO,垂足为E,则CE=
| ||
| 2 |
| 1 |
| 2 |
∴AC=
| CE2+AE2 |
| 2 |
故答案为:
| 2 |
点评:本题考查空间距离的计算,考查线面角,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
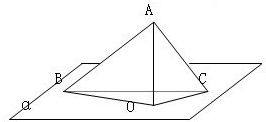 如图所示,A∉平面α,AB、AC是平面α的两条斜线,O是A在平面α内的射影,AO=4,OC=
如图所示,A∉平面α,AB、AC是平面α的两条斜线,O是A在平面α内的射影,AO=4,OC=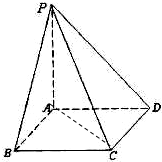 如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,
如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,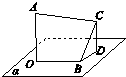 如图所示,AO⊥平面α,BC⊥OB,BC与平面α的夹角为30°,AO=BO=BC=a,则AC=________.
如图所示,AO⊥平面α,BC⊥OB,BC与平面α的夹角为30°,AO=BO=BC=a,则AC=________.