题目内容
已知椭圆D: 的左焦点为F,其左右顶点为A、C,椭圆与y轴正半轴的交点为B,△FBC的外接圆的圆心P(m,n)在直线x+y=0上.
的左焦点为F,其左右顶点为A、C,椭圆与y轴正半轴的交点为B,△FBC的外接圆的圆心P(m,n)在直线x+y=0上.(Ⅰ)求椭圆D的方程;
(Ⅱ)已知直线
 ,N是椭圆D上的动点,NM⊥l,垂足为M,是否存在点N,使得△FMN为等腰三角形?若存在,求出点N的坐标,若不存在,请说明理由.
,N是椭圆D上的动点,NM⊥l,垂足为M,是否存在点N,使得△FMN为等腰三角形?若存在,求出点N的坐标,若不存在,请说明理由.
【答案】分析:(Ⅰ)求出FC的垂直平分线方程,BC的垂直平分线的方程,从而可得P的坐标,利用P(m,n)在直线x+y=0上,结合b2=1-c2,即可求得椭圆D的方程;
(Ⅱ)设N(x,y),求出|MN|,|FN|,|MF|,利用△FMN为等腰三角形,分类讨论,即可求得点N的坐标.
解答:解:(Ⅰ)由题意知,圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,
设F的坐标为(-c,0)(c>0),则FC的垂直平分线方程为 …①
…①
因为BC的中点坐标为 ,BC的斜率为-b
,BC的斜率为-b
所以BC的垂直平分线的方程为 …②
…②
联立①②解得: ,
,
即 ,
,
因为P(m,n)在直线x+y=0上,所以 …(4分)
…(4分)
即(1+b)(b-c)=0
因为1+b>0,所以b=c
再由b2=1-c2求得
所以椭圆D的方程为x2+2y2=1…(7分)
(Ⅱ)由(Ⅰ)知:F ,椭圆上的点横坐标满足-1≤x≤1
,椭圆上的点横坐标满足-1≤x≤1
设N(x,y),由题意得M ,则|MN|=
,则|MN|= ,|FN|=
,|FN|= ,|MF|=
,|MF|=
①若|MN|=|FN|,即 =
=
与x2+2y2=1联立,解得 ,显然不符合条件…(9分)
,显然不符合条件…(9分)
②|MN|=|MF|,即
与x2+2y2=1联立,解得: (显然不符合条件,舍去)
(显然不符合条件,舍去)
所以满足条件的点N的坐标为 …(11分)
…(11分)
③若|FN|=|MF|,即 =
=
解得x=0, (显然不符合条件,舍去)
(显然不符合条件,舍去)
此时所以满足条件的点N的坐标为 …(13分)
…(13分)
综上,存在点N 或
或 ,使得△FMN为等腰三角形…(14分)
,使得△FMN为等腰三角形…(14分)
点评:本题考查椭圆的标准方程,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.
(Ⅱ)设N(x,y),求出|MN|,|FN|,|MF|,利用△FMN为等腰三角形,分类讨论,即可求得点N的坐标.
解答:解:(Ⅰ)由题意知,圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,
设F的坐标为(-c,0)(c>0),则FC的垂直平分线方程为
 …①
…①因为BC的中点坐标为
 ,BC的斜率为-b
,BC的斜率为-b所以BC的垂直平分线的方程为
 …②
…②联立①②解得:
 ,
,
即
 ,
,
因为P(m,n)在直线x+y=0上,所以
 …(4分)
…(4分)即(1+b)(b-c)=0
因为1+b>0,所以b=c
再由b2=1-c2求得

所以椭圆D的方程为x2+2y2=1…(7分)
(Ⅱ)由(Ⅰ)知:F
 ,椭圆上的点横坐标满足-1≤x≤1
,椭圆上的点横坐标满足-1≤x≤1设N(x,y),由题意得M
 ,则|MN|=
,则|MN|= ,|FN|=
,|FN|= ,|MF|=
,|MF|=
①若|MN|=|FN|,即
 =
=
与x2+2y2=1联立,解得
 ,显然不符合条件…(9分)
,显然不符合条件…(9分)②|MN|=|MF|,即

与x2+2y2=1联立,解得:
 (显然不符合条件,舍去)
(显然不符合条件,舍去)所以满足条件的点N的坐标为
 …(11分)
…(11分)③若|FN|=|MF|,即
 =
=
解得x=0,
 (显然不符合条件,舍去)
(显然不符合条件,舍去)此时所以满足条件的点N的坐标为
 …(13分)
…(13分)综上,存在点N
 或
或 ,使得△FMN为等腰三角形…(14分)
,使得△FMN为等腰三角形…(14分)点评:本题考查椭圆的标准方程,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
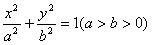 的左焦点F1(
的左焦点F1(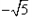 ,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F。
,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F。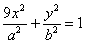 ,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连结MN,试问当k为何值时,直线MN过椭圆G的顶点?
,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连结MN,试问当k为何值时,直线MN过椭圆G的顶点?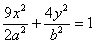 于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB。
于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB。 的左焦点F,C与过原点的直线相交于A,B两点,连结AF,BF,若|AB|=10,|AF|=6,
的左焦点F,C与过原点的直线相交于A,B两点,连结AF,BF,若|AB|=10,|AF|=6, ,则C的离心率为( )
,则C的离心率为( )



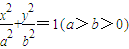 的左焦点
的左焦点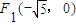 ,若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F.
,若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F.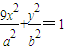 ,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连接MN,试问当k为何值时,直线MN过椭圆G的顶点?
,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连接MN,试问当k为何值时,直线MN过椭圆G的顶点?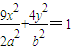 于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC并延长交椭圆W于B,求证:PA⊥PB.
于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC并延长交椭圆W于B,求证:PA⊥PB.