题目内容
已知椭圆E: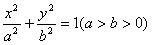 的左焦点F1(
的左焦点F1(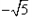 ,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F。
,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F。
(Ⅰ)求椭圆E的方程;
(Ⅱ)已知两点Q(-2,0),M(0,1)及椭圆G: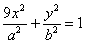 ,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连结MN,试问当k为何值时,直线MN过椭圆G的顶点?
,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连结MN,试问当k为何值时,直线MN过椭圆G的顶点?
(Ⅲ)过坐标原点O的直线交椭圆W: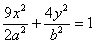 于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB。
于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB。
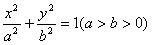 的左焦点F1(
的左焦点F1(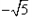 ,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F。
,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F。(Ⅰ)求椭圆E的方程;
(Ⅱ)已知两点Q(-2,0),M(0,1)及椭圆G:
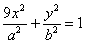 ,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连结MN,试问当k为何值时,直线MN过椭圆G的顶点?
,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连结MN,试问当k为何值时,直线MN过椭圆G的顶点?(Ⅲ)过坐标原点O的直线交椭圆W:
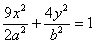 于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB。
于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB。解:(Ⅰ)连接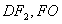 (O为坐标原点,
(O为坐标原点,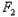 为右焦点),
为右焦点),
由题意知:椭圆的右焦点为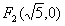 ,
,
因为FO是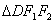 的中位线,且
的中位线,且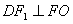 ,
,
所以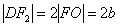 ,
,
所以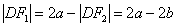 ,
,
故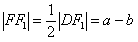 ,
,
在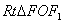 中,
中,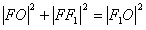 ,
,
即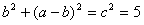 ,
,
又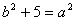 ,
,
解得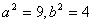 ,
,
所求椭圆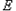 的方程为
的方程为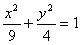 。
。
(Ⅱ)由(Ⅰ)得椭圆G: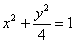 ,
,
设直线l的方程为y=k(x+2)并代入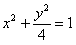 ,
,
整理得: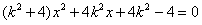 ,
,
由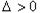 得:
得: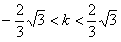 ,
,
设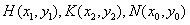 ,
,
则由中点坐标公式得: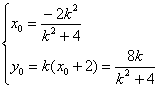 ,
,
①当k=0时,有N(0,0),直线MN显然过椭圆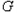 的两个顶点
的两个顶点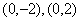 ;
;
②当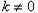 时,则
时,则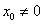 ,直线
,直线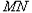 的方程为
的方程为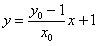 ,
,
此时直线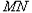 显然不能过椭圆
显然不能过椭圆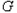 的两个顶点
的两个顶点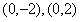 ;
;
若直线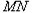 过椭圆
过椭圆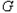 的顶点
的顶点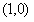 ,
,
则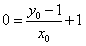 ,即
,即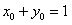 ,
,
所以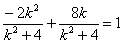 ,解得:
,解得: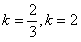 (舍去);
(舍去);
若直线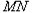 过椭圆
过椭圆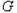 的顶点
的顶点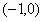 ,
,
则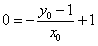 ,即
,即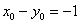 ,
,
所以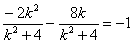 ,解得:
,解得: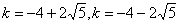 (舍去);
(舍去);
综上,当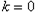 或
或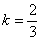 或
或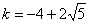 时, 直线
时, 直线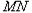 过椭圆
过椭圆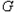 的顶点。
的顶点。
(Ⅲ)由(Ⅰ)得椭圆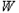 的方程为
的方程为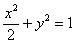 ,
,
根据题意可设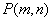 ,则
,则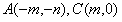 ,
,
则直线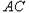 的方程为
的方程为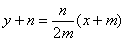 ,…①
,…①
过点P且与AP垂直的直线方程为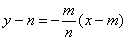 ,…②
,…②
①×②并整理得: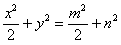 ,
,
又P在椭圆W上,
所以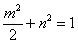 ,所以
,所以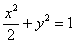 ,
,
即①、②两直线的交点B在椭圆W上,
所以PA⊥PB。
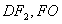 (O为坐标原点,
(O为坐标原点,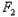 为右焦点),
为右焦点),由题意知:椭圆的右焦点为
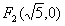 ,
,因为FO是
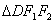 的中位线,且
的中位线,且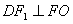 ,
,所以
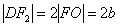 ,
,所以
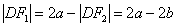 ,
,故
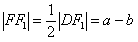 ,
,在
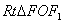 中,
中,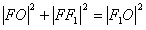 ,
,即
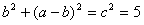 ,
,又
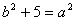 ,
,解得
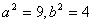 ,
,所求椭圆
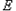 的方程为
的方程为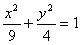 。
。(Ⅱ)由(Ⅰ)得椭圆G:
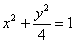 ,
,设直线l的方程为y=k(x+2)并代入
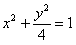 ,
,整理得:
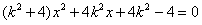 ,
,由
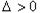 得:
得: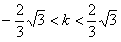 ,
,设
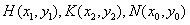 ,
,则由中点坐标公式得:
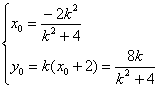 ,
,①当k=0时,有N(0,0),直线MN显然过椭圆
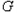 的两个顶点
的两个顶点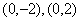 ;
;②当
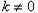 时,则
时,则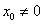 ,直线
,直线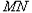 的方程为
的方程为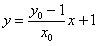 ,
,此时直线
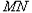 显然不能过椭圆
显然不能过椭圆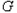 的两个顶点
的两个顶点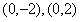 ;
;若直线
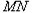 过椭圆
过椭圆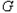 的顶点
的顶点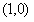 ,
,则
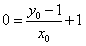 ,即
,即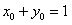 ,
,所以
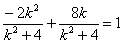 ,解得:
,解得: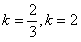 (舍去);
(舍去);若直线
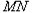 过椭圆
过椭圆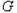 的顶点
的顶点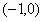 ,
,则
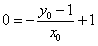 ,即
,即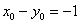 ,
,所以
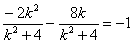 ,解得:
,解得: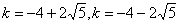 (舍去);
(舍去);综上,当
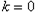 或
或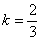 或
或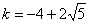 时, 直线
时, 直线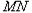 过椭圆
过椭圆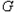 的顶点。
的顶点。(Ⅲ)由(Ⅰ)得椭圆
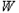 的方程为
的方程为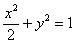 ,
,根据题意可设
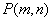 ,则
,则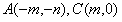 ,
,则直线
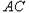 的方程为
的方程为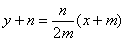 ,…①
,…①过点P且与AP垂直的直线方程为
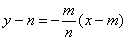 ,…②
,…②①×②并整理得:
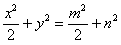 ,
,又P在椭圆W上,
所以
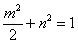 ,所以
,所以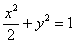 ,
,即①、②两直线的交点B在椭圆W上,
所以PA⊥PB。

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
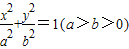 的左顶点为A,左、右焦点分别为F1、F2,且圆C:
的左顶点为A,左、右焦点分别为F1、F2,且圆C: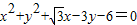 过A,F2两点.
过A,F2两点.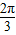 时,证明:点P在一定圆上.
时,证明:点P在一定圆上.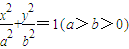 的左焦点
的左焦点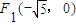 ,若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F.
,若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F.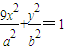 ,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连接MN,试问当k为何值时,直线MN过椭圆G的顶点?
,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连接MN,试问当k为何值时,直线MN过椭圆G的顶点?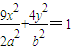 于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC并延长交椭圆W于B,求证:PA⊥PB.
于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC并延长交椭圆W于B,求证:PA⊥PB.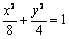 的左焦点为F,左准线
的左焦点为F,左准线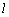 与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.
与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.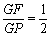 ?若存在,求出点P坐标;若不存在,请说明理由.
?若存在,求出点P坐标;若不存在,请说明理由.