题目内容
某单位建造一间地面面积为12![]() 的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度
的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度![]() 不得超过
不得超过![]() 米,房屋正面的造价为400元/
米,房屋正面的造价为400元/![]() ,房屋侧面的造价为l50元/
,房屋侧面的造价为l50元/![]() ,屋顶和地面的造价费用合计为5800元,如果墙高为3
,屋顶和地面的造价费用合计为5800元,如果墙高为3![]() ,且不计房屋背面的费用。
,且不计房屋背面的费用。
(1)把房屋总造价![]() 表示成
表示成![]() 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;
(2)当侧面的长度为多少时,总造价最底?最低总造价是多少?
解:(1)由题意可得,![]()
=![]()
(2)![]()
当且仅当![]() 即
即![]() 时取等号。
时取等号。
若![]() ,
,![]() 时,有最小值
时,有最小值![]() 。
。
若![]() ,任取
,任取![]() 且
且![]()
![]()
=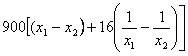
=![]()
∵![]() ,∴
,∴![]() ,
,![]()
∴![]() ,∴
,∴![]() 在
在![]() 上是减函数。
上是减函数。
∴当![]() 时,
时,![]() 有最小值
有最小值![]()
综上:(1)若![]() ,当侧面的长度为
,当侧面的长度为![]() 米时,总造价最低,最低总造价是
米时,总造价最低,最低总造价是![]() 元。
元。
(2)当![]() 时,当侧面的长度为
时,当侧面的长度为![]() 米时,总造价最低,最低总造价是
米时,总造价最低,最低总造价是![]() 元
元
注:本题也可以利用导数判断函数的单调性。

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 (2008•宝坻区一模)某单位建造一间地面面积为12m2的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过a米,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.
(2008•宝坻区一模)某单位建造一间地面面积为12m2的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过a米,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用. 的背面靠墙的矩形小屋,房屋正面的造价为1200元/
的背面靠墙的矩形小屋,房屋正面的造价为1200元/