题目内容
在△ABC,设角A,B,C的对边分别为a,b,c,且 =
= ,则角B= .
,则角B= .
【答案】分析:利用正弦定理将 转化为
转化为 ,再利用两角和与差的正弦函数即可求得角B.
,再利用两角和与差的正弦函数即可求得角B.
解答:解:∵在△ABC, =
= ,由正弦定理
,由正弦定理 =
= =
= =2R得:
=2R得: =
= ,
,
∴ =
= ,
,
∴sinBcosC=2sinAcosB-sinCcosB,
∴sin(B+C)=2sinAcosB,又在△ABC,B+C=π-A,
∴sin(B+C)=sinA≠0,
∴cosB= ,又B∈(0,π),
,又B∈(0,π),
∴B= .
.
故答案为: .
.
点评:本题考查正弦定理与两角和与差的正弦,考查转化思想与运算能力,属于中档题.
 转化为
转化为 ,再利用两角和与差的正弦函数即可求得角B.
,再利用两角和与差的正弦函数即可求得角B.解答:解:∵在△ABC,
 =
= ,由正弦定理
,由正弦定理 =
= =
= =2R得:
=2R得: =
= ,
,∴
 =
= ,
,∴sinBcosC=2sinAcosB-sinCcosB,
∴sin(B+C)=2sinAcosB,又在△ABC,B+C=π-A,
∴sin(B+C)=sinA≠0,
∴cosB=
 ,又B∈(0,π),
,又B∈(0,π),∴B=
 .
.故答案为:
 .
.点评:本题考查正弦定理与两角和与差的正弦,考查转化思想与运算能力,属于中档题.

练习册系列答案
相关题目
在△ABC中设角A,B,C所对的边长分别为a,b,c,且
=
,则角B=( )
| cosC |
| cosB |
| 2a-c |
| b |
| A、30° | B、60° |
| C、90° | D、120° |
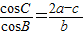 ,则角B=( )
,则角B=( )