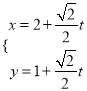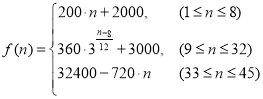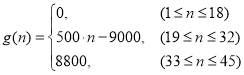题目内容
【题目】在①函数
的图象向右平移
个单位长度得到
的图象，图象关于原点对称；②向量
，
；③函数
这三个条件中任选一个，补充在下面问题中，并解答．已知_________，函数
的图象相邻两条对称轴之间的距离为
．
（1）若
且
，求
的值；
（2）求函数在
上的单调递减区间．
【答案】（1）答案不唯一，见解析 （2）
【解析】
由题意可得函数
的周期
，
选①，可得
，得
，根据函数
图象关于原点对称可求出
，从而求出
；
选②，可得
，从而有；
选③，可得
，从而有；
（1）由
得
，则
；
（2）由
可得函数在
上的单调递减区间．
解：方案一：选条件①
由题意可知，
，
，
，
又函数图象关于原点对称，
，
，
，
，
（1）
，
，
；
（2）由，得
，
令
，得
，令
，得
，
函数在上的单调递减区间为
．
方案二：选条件②
，
，
又，，，
（1），，；
（2）由，得，
令，得，令，得，
函数在上的单调递减区间为．
方案三：选条件③
，
又，，，
（1），，；
（2）由，得，
令，得，令，得.
函数在上的单调递减区间为．
练习册系列答案
阅读快车系列答案
相关题目
