题目内容
三个共面向量a、b、c两两所成的角相等,且|a|=1,|b|=2,|c|=3,则|a+b+c|等于( )
A、
| ||
| B、6 | ||
C、
| ||
| D、3或6 |
分析:三个共面向量
、
、
两两所成的角相等,两个向量所成的角是120°或三个向量的夹角是0°,分两种情况对三个向量的和的模长进行讨论,得到两种不同的结果.
| a |
| b |
| c |
解答:解:∵三个共面向量
、
、
两两所成的角相等,
∴两个向量所成的角是120°或三个向量的夹角是0°
当三个向量的夹角是120°时,
∵|
|=1,|
|=2,|
|=3,
∴|
+
+
|=
=
=
,
当三个向量的夹角是0°时,
|
+
+
|=1+2+3=6,
总上可知,向量的模长是6或
,
故选C.
| a |
| b |
| c |
∴两个向量所成的角是120°或三个向量的夹角是0°
当三个向量的夹角是120°时,
∵|
| a |
| b |
| c |
∴|
| a |
| b |
| c |
|
=
| 1+4+9-2-3-6 |
| 3 |
当三个向量的夹角是0°时,
|
| a |
| b |
| c |
总上可知,向量的模长是6或
| 3 |
故选C.
点评:本题考查向量的模长,在本题所给的条件中容易漏掉一种情况,即三个向量的夹角是0度,即三个向量的方向相同时的模长.

练习册系列答案
相关题目
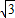
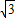 或6
或6
 或6
或6