题目内容
三个共面向量
,
,
两两所成的角相等,且|
|=1,|
|=2,|
|=3,则|
+
+
|=
或6
或6.
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| 3 |
| 3 |
分析:通过分类讨论和利用向量的模的计算公式即可求出.
解答:解:∵三个共面向量
,
,
两两所成的角相等,∴它们所成的角为0或
.
①当它们所成的角为0时,则|
+
+
|=|
|+|
|+|
|=1+2+3=6;
②当它们所成的角为
时,则|
+
+
|=
=
=
=
.
故答案为
或6
| a |
| b |
| c |
| 2π |
| 3 |
①当它们所成的角为0时,则|
| a |
| b |
| c |
| a |
| b |
| c |
②当它们所成的角为
| 2π |
| 3 |
| a |
| b |
| c |
(
|
|
12+22+32+2×(-
|
| 3 |
故答案为
| 3 |
点评:熟练掌握分类讨论思想方法和向量的模的计算公式是解题的关键.

练习册系列答案
相关题目
三个共面向量a、b、c两两所成的角相等,且|a|=1,|b|=2,|c|=3,则|a+b+c|等于( )
A、
| ||
| B、6 | ||
C、
| ||
| D、3或6 |
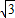
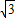 或6
或6
 或6
或6