题目内容
2.已知三棱锥P-ABC的外接球的球心O在AB上,且PO⊥平面ABC,AB=2$\sqrt{3}$,AC=2,则三棱锥P-ABC的体积为$\frac{2\sqrt{6}}{3}$.分析 如图所示,由于三棱锥P-ABC的外接球的球心O在AB上,且PO⊥平面ABC,可得PO是三棱锥P-ABC的高,AC⊥BC.求出BC,利用三棱锥的体积计算公式可得结论.
解答  解:如图所示,
解:如图所示,
∵三棱锥P-ABC的外接球的球心O在AB上,且PO⊥平面ABC,
∴PO是三棱锥P-ABC的高,
∴∠ACB=90°,
∴AC⊥BC.
∵AB=2$\sqrt{3}$,AC=2,
∴BC=2$\sqrt{2}$,
∴VP-ABC=$\frac{1}{3}×\frac{1}{2}×2×2\sqrt{2}×\sqrt{3}$=$\frac{2\sqrt{6}}{3}$,
故答案为:$\frac{2\sqrt{6}}{3}$.
点评 本题考查了线面垂直的性质、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
13.从6本不同的文学书和4本不同的科技书中,任意取出三本,则取到三本同类书的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{10}$ |
10.函数f(x)=$\sqrt{4{x}^{2}+4x+2}$+$\sqrt{4{x}^{2}-12x+13}$的值域是( )
| A. | [3,+∞) | B. | [5,+∞) | C. | [$\sqrt{2}$+$\sqrt{13}$,+∞) | D. | [6,+∞) |
11.计算:(-a3)2=( )
| A. | -a6 | B. | a6 | C. | a5 | D. | a9 |
16.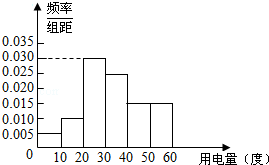 某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:
某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:
(1)求月均用电量的中位数与平均数估计值;
(2)如果用分层抽样的方法从这n位居民中抽取8位居民,再从这8位居民中选2位居民,那么至少有1位居民月均用电量在30至40度的概率是多少?
(3)用样本估计总体,把频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用电量在30至40度的居民数X的分布列.
 某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:
某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:| 分 组 | 频 数 | 频 率 |
| [0,10) | 0.05 | |
| [10,20) | 0.10 | |
| [20,30) | 30 | |
| [30,40) | 0.25 | |
| [40,50) | 0.15 | |
| [50,60] | 15 | |
| 合 计 | n | 1 |
(2)如果用分层抽样的方法从这n位居民中抽取8位居民,再从这8位居民中选2位居民,那么至少有1位居民月均用电量在30至40度的概率是多少?
(3)用样本估计总体,把频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用电量在30至40度的居民数X的分布列.