题目内容
13.设函数f(x)=x3+x,若0≤θ≤$\frac{π}{2}$时,f(sinθ)+f(1-m)>0恒成立,则实数m的取值范围是(-∞,1).分析 利用奇函数f(x)=x3+x单调递增的性质,可将不等式f(sinθ)+f(1-m)>0恒成立,转化为sinθ>m-1恒成立,由0≤θ≤$\frac{π}{2}$,可求得实数m的取值范围.
解答 解:∵f(x)=x3+x,
∴f(-x)=(-x)3+(-x)=-x3-x=-f(x),
∴函数f(x)=x3+x为奇函数;
又f′(x)=3x2+1>0,
∴函数f(x)=x3+x为R上的单调递增函数.
∴f(sinθ)+f(1-m)>0恒成立?f(sinθ)>-f(1-m)=f(m-1)恒成立,
∴sinθ>m-1(0≤θ≤$\frac{π}{2}$)恒成立?m<sinθ+1恒成立,
由0≤θ≤$\frac{π}{2}$知,0≤sinθ≤1,1≤1+sinθ≤2,
故m∈(-∞,1),
故答案为:(-∞,1).
点评 本题考查函数的奇偶性与单调性,突出考查转化思想与恒成立问题,属于中档题.

练习册系列答案
相关题目
18.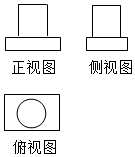 如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
 如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )| A. | 两个长方体 | B. | 两个圆柱 | ||
| C. | 一个长方体和一个圆柱 | D. | 一个球和一个长方体 |
4.已知 f (x)=sin(x+$\frac{π}{2}$),g(x)=sin(π-x),则下列结论中正确的是( )
| A. | 函数 y=f (x)•g ( x) 的周期为 2 | |
| B. | 函数 y=f (x)•g ( x) 的最大值为 1 | |
| C. | 将f (x)的图象向左平移$\frac{π}{2}$个单位后得到 g(x)的图象 | |
| D. | y=f(x)+g(x)的一个对称中心是($\frac{3}{4}π$,0) |
8.某数学学习兴趣小组共5人,其中女生2人,现从该小组中任选3人参加数学竞赛,用ξ表示这3人中女生的人数,则P(ξ≤1)等于( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |
18.设集合U={1,2,3,4,5,6,7},集合A={1,2,5,7},则∁UA=( )
| A. | {1,2,5,7} | B. | {3,4,6} | C. | {6} | D. | U |
5.三棱锥P-ABC的四个顶点都在球O的表面上,PA⊥平面ABC,AB⊥BC,PA=2,AB=BC=1,则球O的表面积为( )
| A. | $\sqrt{6}$π | B. | 6π | C. | 24π | D. | 2$\sqrt{6}$π |
13.已知A-BCD为正四面体,则其侧面与底面所成角的余弦值为( )
| A. | $\frac{1}{3}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{2}$ | D. | $\frac{2\sqrt{2}}{3}$ |