题目内容
在数列{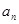 }中,
}中,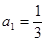 ,并且对任意
,并且对任意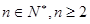 都有
都有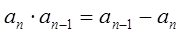 成立,令
成立,令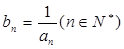 .
.
(Ⅰ)求数列{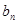 }的通项公式;
}的通项公式;
(Ⅱ)设数列{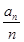 }的前n项和为
}的前n项和为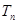 ,证明:
,证明: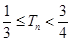
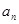 }中,
}中,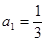 ,并且对任意
,并且对任意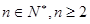 都有
都有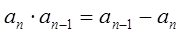 成立,令
成立,令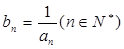 .
.(Ⅰ)求数列{
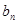 }的通项公式;
}的通项公式;(Ⅱ)设数列{
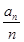 }的前n项和为
}的前n项和为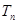 ,证明:
,证明: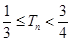
(Ⅰ)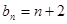
(Ⅱ)见解析
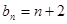
(Ⅱ)见解析
试题分析:(I)、当n=1时,先求出b1=3,当n≥2时,求得b n+1与bn的关系即可知道bn为等差数列,然后便可求出数列{bn}的通项公式;
(II)根据(I)中求得的bn的通项公式先求出数列{
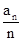 }的表达式,然后求出Tn的表达式,根据不等式的性质即可证明
}的表达式,然后求出Tn的表达式,根据不等式的性质即可证明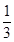 <Tn<
<Tn<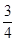
解:(Ⅰ)当n=1时,
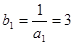 ,当
,当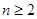 时,
时,由
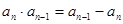 得
得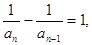 所以
所以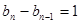 ------------4分
------------4分所以数列
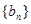 是首项为3,公差为1的等差数列,
是首项为3,公差为1的等差数列,所以数列
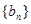 的通项公式为
的通项公式为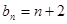 -------------5分
-------------5分(Ⅱ)
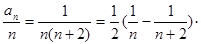 ------------------------------------7分
------------------------------------7分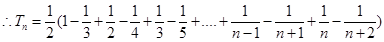 -------------------11分
-------------------11分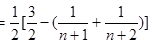
可知Tn是关于变量n的增函数,当n趋近无穷大时,
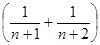 的值趋近于0,
的值趋近于0,当n=1时Tn取最小值
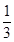 ,故有
,故有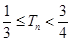 ----------------14分
----------------14分点评:解决该试题的关键是运用整体的思想来表示出递推关系,然后进而利用函数的单调性的思想来放缩得到证明。

练习册系列答案
相关题目
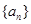 的首项
的首项 ,
,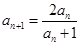 ,
,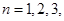 ….
….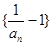 是等比数列;
是等比数列;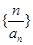 的前
的前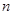 项和
项和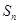 .
.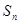 是等差数列
是等差数列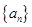
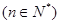 的前
的前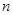 项和,且
项和,且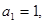
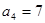 ,则
,则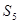 =
= 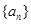 中,
中,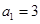 ,前
,前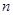 项和为
项和为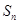 ,等比数列
,等比数列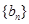 各项均为正数,
各项均为正数,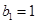 ,且
,且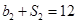 ,
,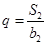 .
.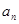 与
与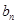 ;(2)求
;(2)求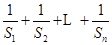 .
.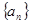 中,已知
中,已知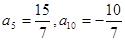 。
。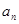 和前n项和
和前n项和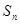 ;
;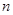 的值;
的值;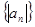 的前n项和
的前n项和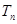 .
.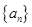 的前
的前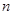 项和为
项和为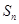 ,且满足
,且满足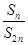 为常数,则称该数列为
为常数,则称该数列为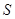 数列.
数列.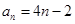 是否为
是否为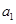 且公差不为零的等差数列
且公差不为零的等差数列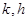 满足
满足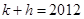 ,求
,求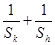 的最小值
的最小值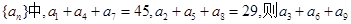 等于 ( )
等于 ( )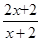 ,若数列
,若数列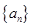 ,
,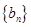 满足
满足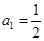 ,
,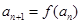 ,
,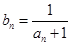
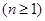 ,
,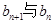 的关系,并求数列
的关系,并求数列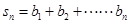 , 若
, 若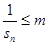 恒成立.求
恒成立.求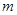 的最小值.
的最小值.