题目内容
(本小题满分12分)
定义在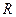 上的增函数
上的增函数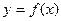 对任意
对任意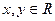 都有
都有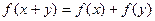 。
。
(1)求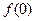 ;
;
(2)求证: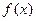 为奇函数;
为奇函数;
(3)若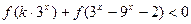 对任意
对任意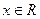 恒成立,求实数
恒成立,求实数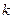 的取值范围。
的取值范围。
定义在
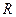 上的增函数
上的增函数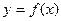 对任意
对任意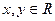 都有
都有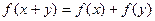 。
。(1)求
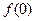 ;
;(2)求证:
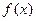 为奇函数;
为奇函数;(3)若
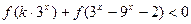 对任意
对任意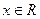 恒成立,求实数
恒成立,求实数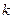 的取值范围。
的取值范围。(1)0
(2)略
(3)
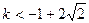
解(1)令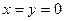 ,得
,得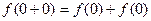 ,即
,即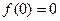 。
。
(2)证明:令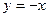 ,得
,得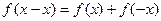 ,
,
又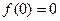 ,则有
,则有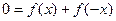 。
。
即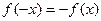 对任意
对任意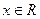 成立,
成立,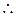
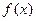 为奇函数。
为奇函数。
(3)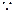
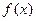 在
在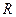 上是增函数,又由(2)知
上是增函数,又由(2)知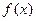 为奇函数。
为奇函数。
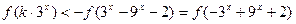 ,
,
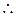
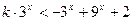 ,
,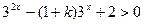 对任意
对任意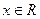 恒成立。
恒成立。
令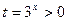 ,问题等价于
,问题等价于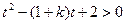 对任意
对任意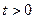 恒成立。
恒成立。
令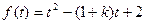 ,其对称轴为
,其对称轴为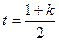 ,
,
当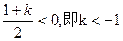 时,
时,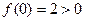 ,符合题意;
,符合题意;
当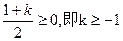 时,对任意
时,对任意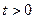 ,
,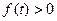 恒成立
恒成立
解得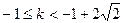 。
。
综上所述,当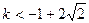 时,
时,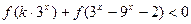 对任意
对任意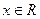 恒成立。
恒成立。
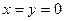 ,得
,得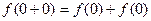 ,即
,即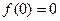 。
。(2)证明:令
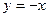 ,得
,得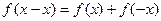 ,
,又
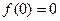 ,则有
,则有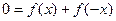 。
。即
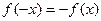 对任意
对任意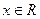 成立,
成立,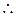
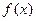 为奇函数。
为奇函数。(3)
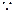
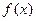 在
在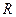 上是增函数,又由(2)知
上是增函数,又由(2)知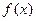 为奇函数。
为奇函数。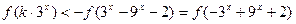 ,
,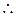
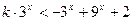 ,
,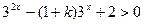 对任意
对任意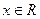 恒成立。
恒成立。令
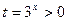 ,问题等价于
,问题等价于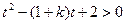 对任意
对任意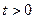 恒成立。
恒成立。令
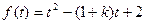 ,其对称轴为
,其对称轴为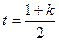 ,
,当
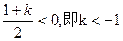 时,
时,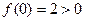 ,符合题意;
,符合题意;当
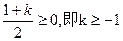 时,对任意
时,对任意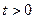 ,
,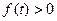 恒成立
恒成立
解得
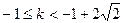 。
。综上所述,当
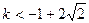 时,
时,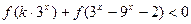 对任意
对任意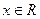 恒成立。
恒成立。
练习册系列答案
相关题目
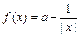 .
.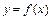 在
在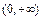 上的单调性,不用证明;
上的单调性,不用证明;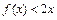 在
在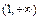 上恒成立,求实数
上恒成立,求实数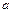 的取值范围;
的取值范围;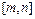 上的值域是
上的值域是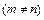 ,求实数
,求实数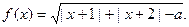
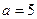 时,求函数
时,求函数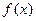 的定义域;
的定义域;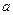 的取值范围.
的取值范围.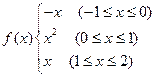
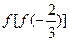 的值;
的值;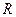 上的偶函数
上的偶函数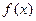 满足
满足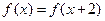 ,当
,当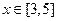 时,
时,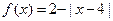 ,则下列错误的是
,则下列错误的是



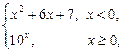 则 f (0)+f (
则 f (0)+f (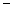 1)=
1)=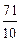
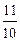
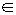 D,存在正数k,有|f(x)|≤k|x|成立,则称函数f(x)是D上的“倍约束函数”,已知下列函数:(1)f(x)=2x; (2)f(x)=Sin(x+
D,存在正数k,有|f(x)|≤k|x|成立,则称函数f(x)是D上的“倍约束函数”,已知下列函数:(1)f(x)=2x; (2)f(x)=Sin(x+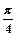 );(3)f(x)=
);(3)f(x)=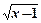 ;(4)f(x)=
;(4)f(x)=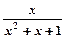 ;其中是“倍约束函数”的是( )
;其中是“倍约束函数”的是( ) -x-1 C f(x)=x3-x+1 D f(x)=-x3-x+1
-x-1 C f(x)=x3-x+1 D f(x)=-x3-x+1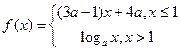 是
是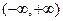 上的减函数,那么
上的减函数,那么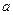 的取值范围是
的取值范围是