题目内容
19.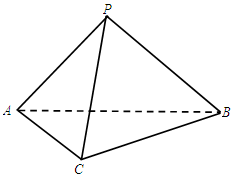 如图,在三棱锥P-ABC中,AC=BC=2,AP=BP=AB,BC⊥平面PAC.
如图,在三棱锥P-ABC中,AC=BC=2,AP=BP=AB,BC⊥平面PAC.(Ⅰ)求证:PC⊥AB;
(Ⅱ)求三棱锥P-ABC的体积.
(Ⅲ)(理科做,文科不做)求二面角B-AP-C的正弦值.
分析 (Ⅰ)取AB中点D,连结PD、CD.由已知可得PD⊥AB且CD⊥AB.然后利用线面垂直的判定可得AB⊥平面PCD.进一步得到PC⊥AB;
(Ⅱ)由BC⊥平面PAC,得BC⊥AC,BC⊥PC,求解三角形可得AC⊥PC.求出三角形APC的面积,然后利用等积法求得三棱锥P-ABC的体积;
(Ⅲ)取AP中点E,连结BE,CE.由题意可证∠BEC是二面角B-AP-C的平面角.然后求解三角形可得sin∠BEC=$\frac{BC}{BE}=\frac{\sqrt{6}}{3}$.即二面角B-AP-C的正弦值为$\frac{\sqrt{6}}{3}$.
解答 (Ⅰ)证明:取AB中点D,连结PD、CD.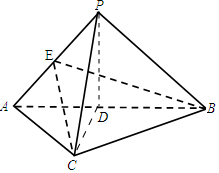
∵AP=BP,∴PD⊥AB.
∵AC=BC,∴CD⊥AB.
又PD∩CD=D,∴AB⊥平面PCD.
∵PC?平面PCD,∴PC⊥AB;
(Ⅱ)解:∵BC⊥平面PAC,∴BC⊥AC,BC⊥PC,
又AC=BC=2,∴AB=$2\sqrt{2}$,则AB=AP=PB=$2\sqrt{2}$,
∴PC=2,则PC2+AC2=PA2,即AC⊥PC.
∴${S}_{△APC}=\frac{1}{2}×2×2=2$,${V}_{P-ABC}={V}_{B-APC}=\frac{1}{3}•{S}_{△APC}•BC=\frac{1}{3}×2×2=\frac{4}{3}$;
(Ⅲ)解:取AP中点E,连结BE,CE.
∵AP=BP,∴BE⊥AP,
∵BC⊥平面PAC,∴BC⊥AP,
又∵BE∩BC=B,∴AP⊥平面BEC,则AP⊥EC.
∴∠BEC是二面角B-AP-C的平面角.
∵BC⊥平面PAC,∴BC⊥AC,
又∵AC=BC=2,∴AB=2$\sqrt{2}$,
∵AP=BP=AB,∴$BE=\frac{\sqrt{3}}{2}AB=\sqrt{6}$.
∵BC⊥平面PAC,∴BC⊥CE,则∠BCE=90°.
∴在△BCE中,sin∠BEC=$\frac{BC}{BE}=\frac{\sqrt{6}}{3}$.
故二面角B-AP-C的正弦值为$\frac{\sqrt{6}}{3}$.
点评 本题考查线面垂直的判定与性质,考查了二面角的平面角的求法,正确找出二面角的平面角是解题的关键,训练了利用等积法求多面体的体积,属中档题.

| A. | 过直线外一点有且只有一条直线与已知直线平行 | |
| B. | 不公线的三个点确定一个平面 | |
| C. | 如果两条直线垂直于同一条直线,那么这两条直线平行 | |
| D. | 如果两个平面垂直于同一个平面,那么这两个平面可能互相垂直 |
| A. | lnx0 | B. | $ln\sqrt{x_0}$ | C. | ln(lnx0) | D. | ${(ln{x_0})^2}$ |
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{2}$ |
| A. | y=x-2 | B. | $y=\frac{{{x^2}-4}}{x+2}$ | C. | $y=\frac{{{{({x-2})}^2}}}{x-2}$ | D. | $y={({\frac{x-2}{{\sqrt{x-2}}}})^2}$ |