题目内容
(2006
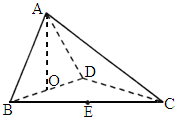
·福建)如下图，四面体ABCD中，O、E分别是BD、BC的中点，CA=CB=CD=BD=2，
．
(1)
求证：AO⊥平面BCD；(2)
求异面直线AB与CD所成角的余弦值；(3)
求点E到平面ACD的距离．
答案：略
解析：
解析：
|
(1) 证明：连接OC．∵ BO=DO，AB=AD，∴AO⊥BD．∵ BO=DO，BC=CD，∴CO⊥BD．在△ AOC中，由已知可得AO=1， ．
而 AC=2，∴  ．
∴∠ AOC=90°，即AO⊥OC．∵  ，
∴ AO⊥平面BCD．(2) 以O为原点，如下图建立空间直角坐标系，
则 B(1，0，0)，D(－1，0，0)， ，A(0，0，1)， ， ， ．
∴  ．
∴异面直线 AB与CD所成角的余弦值是 ．
(3) 设平面ACD的法向量为n=(x，y，z)，则
 ∴
令 y=1，得 是平面ACD的一个法向量．又 ，
∴点 E到平面ACD的距离 ． |
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
的左焦点F，O为坐标原点．
．
