题目内容
如图,在棱长为 的正方体
的正方体 中,
中, 为
为 的中点,
的中点,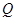 为
为 上任意一点,
上任意一点, 为
为 上两点,且
上两点,且 的长为定值,则下面四个值中不是定值的是( )
的长为定值,则下面四个值中不是定值的是( )
A.点 到平面 到平面 的距离 的距离 |
B.直线 与平面 与平面 所成的角 所成的角 |
C.三棱锥 的体积 的体积 |
D. 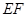 的面积 的面积 |
B.
解析试题分析:根据线面平行的性质可以判断A答案是定值;根据线面角的定义,可判断B答案不是定值;根据等底同高的三角形面积相等及A的结论结合棱锥的体积公式,可以判断C答案是定值;根据三角形的面积公式可以判断D答案是定值,进而得到答案.
考点:空间中直线与平面之间的位置关系;棱柱、棱锥、棱台的体积;点、线、面间的距离计算;三角形面积公式.

练习册系列答案
相关题目
直三棱柱 中,
中, ,
, 分别是
分别是 的中点,
的中点, ,则
,则 与
与 所成的角的余弦值为( ).
所成的角的余弦值为( ).
A. | B. | C. | D. |
设 是两个不同的平面,
是两个不同的平面, 是一条直线,以下命题正确的是( )
是一条直线,以下命题正确的是( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
已知 为异面直线,
为异面直线,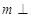 平面
平面 ,
, 平面
平面 .平面α与β外的直线
.平面α与β外的直线 满足
满足 ,则( )
,则( )
A. ,且 ,且 | B. ,且 ,且 |
C. 与 与 相交,且交线垂直于 相交,且交线垂直于 | D. 与 与 相交,且交线平行于 相交,且交线平行于 |
已知二面角 为
为 ,
, ,
, ,A为垂足,
,A为垂足, ,
, ,
, ,则异面直线
,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为
A. | B. | C. | D. |
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是( )
| A.PB⊥AD |
| B.平面PAB⊥平面PBC |
| C.直线BC∥平面PAE |
| D.直线PD与平面ABC所成的角为45° |



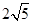
 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点,作
,E是PC的中点,作 交PB于点F.
交PB于点F. 的体积.
的体积.