题目内容
直四棱柱ABCD﹣A1B1C1D1中，底面ABCD是等腰梯形，AB∥CD，AB=2AD=2DC=2，E为
BD1的中点，F为AB中点．
（1）求证：EF∥平面ADD1A1；
（2）若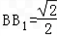
，求A1F与平面DEF所成角的正弦值．
BD1的中点，F为AB中点．
（1）求证：EF∥平面ADD1A1；
（2）若
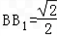，求A1F与平面DEF所成角的正弦值．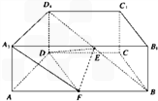
解：（1）证明：连接AD1，在△ABD1中
∵E是BD1的中点，F是BA中点，
∴EF∥AD1又EF
平面ADD1A1，AD1
平面ADD1A1
∴EF∥平面ADD1A1．
（2）建立如图所示的空间直角坐标系D﹣xyzz（DG为AB边上的高）
则有A1（
，﹣
，
），F（
，
，0），D1（0，0，
），B（
，
，0），
∴E（
，
，
），
设平面DEF的一个法向量为n=（x，y，z），
由，
得
取x=1解得
∴法向量
∵
=（0，1，﹣
），
设A1F与平面DEF所成的角为θ，
则
=
∴A1F与平面DEF所成角的正弦值为
．
∵E是BD1的中点，F是BA中点，
∴EF∥AD1又EF
平面ADD1A1，AD1平面ADD1A1∴EF∥平面ADD1A1．
（2）建立如图所示的空间直角坐标系D﹣xyzz（DG为AB边上的高）
则有A1（
，﹣，），F（，，0），D1（0，0，），B（，，0），∴E（
，， ），设平面DEF的一个法向量为n=（x，y，z），
由，
得取x=1解得
∴法向量
∵
=（0，1，﹣），设A1F与平面DEF所成的角为θ，
则
=∴A1F与平面DEF所成角的正弦值为
．
练习册系列答案
相关题目
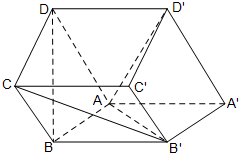如图，在直四棱柱ABCD-A′B′C′D′中，底面ABCD为梯形，BC∥AD，AA′=AB=
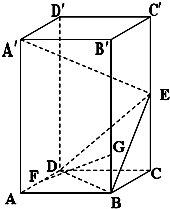已知直四棱柱ABCD-A′B′C′D′，四边形ABCD为正方形，AA′=2AB=2，E为棱CC′的中点．
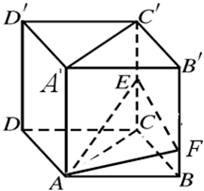已知直四棱柱ABCD-A′B′C′D′的底面是菱形，∠ABC=60°，E、F分别是棱CC′与BB′上的点，且EC=BC=2FB=2．
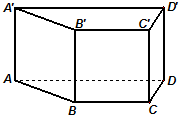在高为1的直四棱柱ABCD-A'B'C'D'中，底面ABCD是等腰梯形，AB=BC=CD=1，AD=2． 
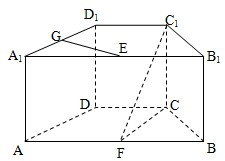（2009•崇明县一模）如图，在直四棱柱ABCD-A'B'C'D'中，底面ABCD为等腰梯形，AB∥CD，AB=4，BC=CD=2，AA1=2，E、F、G分别是棱A1B1、AB、A1D1的中点．