题目内容
已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
 .
.(1)求函数
 的最小正周期;
的最小正周期;(2)求函数
 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.:(1) ;(2)
;(2) ;
; .
.
 ;(2)
;(2) ;
; .
.试题分析:(1)先利用和差化积公式以及二倍角公式,将原式化为
 ,再利用积化和差公式将此式变形化简得到:
,再利用积化和差公式将此式变形化简得到: ,再根据公式:
,再根据公式: ,求出所给函数的周期;(2)根据已知条件
,求出所给函数的周期;(2)根据已知条件 ,求出
,求出 ,再依据函数
,再依据函数 ,在
,在 上的单调性得到:函数
上的单调性得到:函数 在
在 时取得最大值,在
时取得最大值,在 时取得最小值,并分别求出最大值和最小值以及对应的
时取得最小值,并分别求出最大值和最小值以及对应的 的值.
的值.试题解析:(1)





 5分
5分所以
 的最小正周期为
的最小正周期为 . 7分
. 7分(2)由(1)知
 ,
,因为
 ,所以
,所以 .
.当
 ,即
,即 时,函数
时,函数 取最大值
取最大值 ;
;当
 ,即
,即 时,函数
时,函数 取最小值
取最小值 .
.所以,函数
 在区间
在区间 上的最大值为
上的最大值为 ,最小值为
,最小值为 . 13分
. 13分
练习册系列答案
相关题目
 的部分图象如图所示,其中点A为最高点,点B,C为图象与轴的交点,在
的部分图象如图所示,其中点A为最高点,点B,C为图象与轴的交点,在 中,角
中,角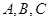 对边为
对边为 ,
, ,且满足
,且满足 .
.
 的单调递增区间.
的单调递增区间. )+
)+ ,x∈R.
,x∈R.
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 是
是 三边长,且
三边长,且 ,
, .求角
.求角 及
及 的值.
的值. x+
x+ )+cos(
)+cos( )的最小正周期为π,且f(-x)=f(x),则( )
)的最小正周期为π,且f(-x)=f(x),则( ) ,
, )单调递减
)单调递减 (
( )的最小正周期为_____,最大值为____.
)的最小正周期为_____,最大值为____. 在区间
在区间 内的所有实根之和为.(符号
内的所有实根之和为.(符号 表示不超过
表示不超过 的最大整数)。
的最大整数)。 和点
和点 恰好是函数
恰好是函数 的图象的相邻的对称轴和对称中心,则
的图象的相邻的对称轴和对称中心,则 的表达式可以是
的表达式可以是



 的图象向左平移m个单位(m>0),若所得的图象关于直线x=
的图象向左平移m个单位(m>0),若所得的图象关于直线x= 对称,则m的最小值为( )
对称,则m的最小值为( )

