题目内容
已知向量m=(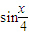 ,
,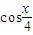 ),n=(
),n=(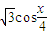 ,
,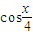 ),记f(x)=m•n;
),记f(x)=m•n;(1)若f(x)=1,求
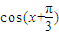 的值;
的值;(2)若△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函
数f(A)的取值范围.
【答案】分析:(1)先根据两角和与差的正弦公式将函数f(x)化简为y=Asin(wx+ρ)+b的形式,根据f(x)=1求出sin( ),再由二倍角公式求出答案.
),再由二倍角公式求出答案.
(2)先根据正弦定理将边的关系转化为角的正弦的关系,再由诱导公式求出cosB得到角B的值,从而可确定角A的范围,再求出 范围,得到f(A)的取值范围.
范围,得到f(A)的取值范围.
解答:解:(1)f(x)=m•n= sin
sin =
= =sin(
=sin( )+
)+ ,
,
∵f(x)=1,∴sin( )=
)= ,
,
∴cos(x+ )=1-2
)=1-2 =
= .
.
(2)∵(2a-c)cosB=bcosC,∴由正弦定理得(2sinA-sinC)cosB=sinBcosC,
∴2sinAcosB-sinCcosB=sinBcosC,∴2sinAcosB=sin(B+C),
∵A+B+C=π,,∴sin(B+C)=sinA,且sinA≠0,
∴cosB= ,B=
,B= ;
;
∴0<A< ,∴
,∴ ,
,
∴ ,
, ;
;
又∵f(x)=sin( )+
)+ ,∴f(A)=sin(
,∴f(A)=sin( )+
)+ ,
,
故函数f(A)的取值范围是(1, ).
).
点评:本题主要考查两角和与差的正弦公式和正弦定理的应用.向量和三角函数的综合题是高考的热点问题,每年必考,要给予充分的重视.
 ),再由二倍角公式求出答案.
),再由二倍角公式求出答案.(2)先根据正弦定理将边的关系转化为角的正弦的关系,再由诱导公式求出cosB得到角B的值,从而可确定角A的范围,再求出
 范围,得到f(A)的取值范围.
范围,得到f(A)的取值范围.解答:解:(1)f(x)=m•n=
 sin
sin =
= =sin(
=sin( )+
)+ ,
,∵f(x)=1,∴sin(
 )=
)= ,
,∴cos(x+
 )=1-2
)=1-2 =
= .
.(2)∵(2a-c)cosB=bcosC,∴由正弦定理得(2sinA-sinC)cosB=sinBcosC,
∴2sinAcosB-sinCcosB=sinBcosC,∴2sinAcosB=sin(B+C),
∵A+B+C=π,,∴sin(B+C)=sinA,且sinA≠0,
∴cosB=
 ,B=
,B= ;
;∴0<A<
 ,∴
,∴ ,
,
∴
 ,
, ;
;又∵f(x)=sin(
 )+
)+ ,∴f(A)=sin(
,∴f(A)=sin( )+
)+ ,
,故函数f(A)的取值范围是(1,
 ).
).点评:本题主要考查两角和与差的正弦公式和正弦定理的应用.向量和三角函数的综合题是高考的热点问题,每年必考,要给予充分的重视.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目